Question

2．如图，已知矩形ABCD的边长分别为3cm，4cm，E、F、G、H分别是AB、BC、CD、DA的中点，则四边形EFGH的面积等于6cm²．

Answer 1

分析 先有矩形的性质和中点，判断出四边形QEGD是矩形，求出EG，再求出FH，最后说明FH⊥EG，即可求出四边形的面积．

解答 解：如图，连接EG，FH，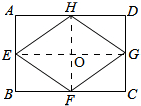

在矩形ABCD中，AB∥CD，AB=CD，∠A=90°
∵点E，G是AB，CD中点，
∴AE=$\frac{1}{2}$AB，DG=$\frac{1}{2}$CD，
∴AE=DG，
∴四边形QEGD是矩形，
∴EG=AD=4
同理：四边形ABFH是矩形，
∴FH=AB=3，
∴四边形AEOH是矩形，
∴EG⊥FH，
∴四边形EFGH的面积等于$\frac{1}{2}$EG×FH=$\frac{1}{2}$×4×3=6cm²．
故答案为：6

点评 此题是中点四边形，主要考查了矩形的性质和判定，中点的定义，对角线互相垂直的四边形的面积的计算方法，解本题的关键是理解对角线互相垂直的四边形的面积的计算方法是两条对角线积的一半．