
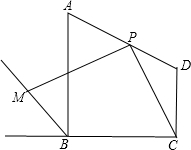
 已知:梯形ABCD中,AB∥CD,P是AD中点,M是梯形ABCD外角∠ABE的平分线上一点,且∠CPM=90°,如图,当∠ABC=90°时,探究PC与PM之间的数量关系.
已知:梯形ABCD中,AB∥CD,P是AD中点,M是梯形ABCD外角∠ABE的平分线上一点,且∠CPM=90°,如图,当∠ABC=90°时,探究PC与PM之间的数量关系. 分析 延长CP交BA的延长线于F,连接MF,CM,过M作MG⊥AB,MH⊥BC,由P是AD中点,得到AP=DP,通过△AFP≌△DCP,得到PF=PC,由∠CPM=90°,得到MF=MC,通过Rt△CMH≌Rt△FMG中,得到∠MFA=∠MCH,于是得到∠MFC=∠MCH+∠FCD=∠MCF,由于∠BCD=90°,得到△MCF是等腰直角三角形,根据等腰直角三角形的性质即可得到结论.
解答 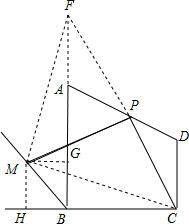 解:PC=PM,
解:PC=PM,
理由:延长CP交BA的延长线于F,连接MF,CM,过M作MG⊥AB,MH⊥BC,
∵P是AD中点,
∴AP=DP,
∵AB∥CD,
∴∠AFP=∠DCP,
在△APF与△DPC中,$\left\{\begin{array}{l}{∠AFP=∠DCP}\\{∠APF=∠DPC}\\{AP=DP}\end{array}\right.$,
∴△AFP≌△DCP,PF=PC,
∵∠CPM=90°,
∴MP⊥CP,
∴MF=MC,
∴∠MFC=∠MCF,
∵MB平分∠HBG,
∴MG=MH,
在Rt△CMH与Rt△FMG中,$\left\{\begin{array}{l}{MC=MF}\\{MH=MG}\end{array}\right.$,
∴Rt△CMH≌Rt△FMG中,
∴∠MFA=∠MCH,
∴∠MFC=∠MCH+∠FCD=∠MCF,
∵∠BCD=90°,
∴∠MCF=∠MFC=45°,
∴△MCF是等腰直角三角形,
∵PF=PC,
∴PM=PC.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质和判定,直角梯形的性质,正确的作出辅助线是解题的关键,


科目:初中数学 来源:2016-2017学年浙江省衢州市八年级下学期第一次月考数学试卷(解析版) 题型:单选题
下列方程是一元二次方程的是( )
A. x2﹣y=1 B. x2+2x﹣3=0 C. 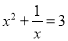 D. x﹣5y=6
D. x﹣5y=6
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对应点到旋转中心的距离相等 | B. | 图形上每一部分旋转的角度相同 | ||
| C. | 旋转前后的两个图形全等 | D. | 图形上每一点所经过的路程相同 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
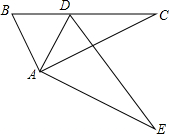 如图,Rt△ABC绕点直角顶点A旋转一定角度后得到△ADE,且点D落在BC上.
如图,Rt△ABC绕点直角顶点A旋转一定角度后得到△ADE,且点D落在BC上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
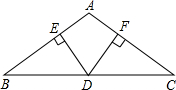 在△ABC中,AB=AC,D是BC边上的点,DE⊥AB于E,DF⊥AC于F.
在△ABC中,AB=AC,D是BC边上的点,DE⊥AB于E,DF⊥AC于F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com