
【题目】如图,抛物线![]() 为常数)交
为常数)交![]() 轴于
轴于![]() 两点.
两点.
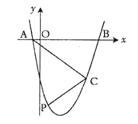
(1)求抛物线的解析式;
(2)直接写出:①抛物线的顶点坐标;
②抛物线与![]() 轴交点关于该抛物线对称轴对称的点
轴交点关于该抛物线对称轴对称的点![]() 的坐标;
的坐标;
(3)在直线![]() 下方的抛物线上是否存在点
下方的抛物线上是否存在点![]() 使
使![]() 的面积最大?若存在,请求出点
的面积最大?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】![]() ;(2)①抛物线的顶点坐标为
;(2)①抛物线的顶点坐标为![]() ,②点
,②点![]() 的坐标为
的坐标为![]() ;(3)在直线
;(3)在直线![]() 下方的抛物线上存在点
下方的抛物线上存在点![]() 使
使![]() 的面积最大.
的面积最大.
【解析】
(1)用待定系数法求抛物线解析式即可;
(2)①将抛物线解析式化成顶点式可得顶点坐标;
②首先求出抛物线与![]() 轴的交点和对称轴,然后可得点
轴的交点和对称轴,然后可得点![]() 的坐标;
的坐标;
(3)设点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,首先求出直线
,首先求出直线![]() 的解析式,表示出点E坐标,得到EP的长,然后根据
的解析式,表示出点E坐标,得到EP的长,然后根据![]() 表示出
表示出![]() 的面积,再利用二次函数的最值求解.
的面积,再利用二次函数的最值求解.
解:(1)由抛物线过![]() 两点知,
两点知,![]() ,
,
解得![]()
∴![]() ;
;
(2)①∵![]() ,
,
∴抛物线的顶点坐标为![]() ;
;
②∵抛物线与![]() 轴交点坐标为:(0,-6),对称轴为:
轴交点坐标为:(0,-6),对称轴为:![]() ,
,
∴点![]() 的坐标为
的坐标为![]()
(3)设点![]() 的坐标为
的坐标为![]() ,
,
直线![]() 的解析式为
的解析式为![]() ,代入
,代入![]() ,
,![]()
可得![]() ,解得
,解得![]() ,
,
∴直线![]() 的解析式为:
的解析式为:![]() ,
,
过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() ,
,
把![]() 代入
代入![]() 得
得![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
![]() ,
,
∴当![]() 时,
时,![]() 有最大值
有最大值![]() ,此时
,此时![]() ,
,
∴点![]() 的坐标是
的坐标是![]() ,
,
因此,在直线![]() 下方的抛物线上存在点
下方的抛物线上存在点![]() 使
使![]() 的面积最大.
的面积最大.


科目:初中数学 来源: 题型:
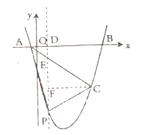
【题目】如图,二次函数 y=ax 2 +bx+c 的图象与 y 轴正半轴相交,其顶点坐标为(![]() ,1).下列结论:①abc<0;②a+b=0;③4ac-b2=4a;④a+b+c<0.其中正确的是( ).
,1).下列结论:①abc<0;②a+b=0;③4ac-b2=4a;④a+b+c<0.其中正确的是( ).

A.①②③④B.②③④C.①②③D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张正面分别写有数字-1,1,2的卡片,它们除数字不同无其它差别,现将这三张卡片背面朝上洗匀后.
(1)随机抽取一张,求抽到数字2的概率;
(2)先随机抽取一张,以其正面数字作为k值,将卡片放回再随机抽一张,以其正面的数字作为b值,请你用恰当的方法表示所有可能的结果,并求出直线y=kx+b的图像不经过第四象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正比例函数y=kx(x≥0)与反比例函数 ![]() (x>0)的图象交于点A(2,3)。
(x>0)的图象交于点A(2,3)。
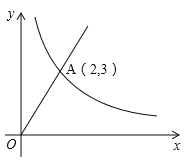
(1)求正比例函数与反比例函数的解析式;
(2)写出正比例函数值大于反比例函数值时自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低![]() 元.
元.
(1)填表:(不需化简)
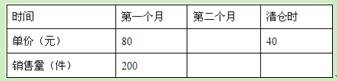
(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出下列结论:①△DAG≌△DFG;②BG=2AG;③△EBF∽△DEG;④S△BEF=![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )
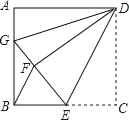
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAB中,∠ABO=90°,点A位于第一象限,点O为坐标原点,点B在x轴正半轴上,若双曲线y=![]() (x>0)与△OAB的边AO.AB分别交于点C.D,点C为AO的中点,连接OD.CD.若S△OBD=3,则S△OCD为_____.
(x>0)与△OAB的边AO.AB分别交于点C.D,点C为AO的中点,连接OD.CD.若S△OBD=3,则S△OCD为_____.
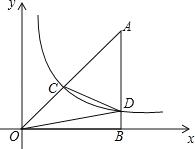
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com