
【题目】如图,二次函数 y=ax 2 +bx+c 的图象与 y 轴正半轴相交,其顶点坐标为(![]() ,1).下列结论:①abc<0;②a+b=0;③4ac-b2=4a;④a+b+c<0.其中正确的是( ).
,1).下列结论:①abc<0;②a+b=0;③4ac-b2=4a;④a+b+c<0.其中正确的是( ).

A.①②③④B.②③④C.①②③D.①②④
【答案】C
【解析】
①根据抛物线开口向下可得出a<0,由抛物线对称轴为x=![]() 可得出b=-a>0,结合抛物线图象可知c>0,进而可得出abc<0,①正确;②由b=-a可得出a+b=0,②正确;③根据抛物线顶点坐标为(-
可得出b=-a>0,结合抛物线图象可知c>0,进而可得出abc<0,①正确;②由b=-a可得出a+b=0,②正确;③根据抛物线顶点坐标为(-![]() ,
,![]() ),由此可得出
),由此可得出![]() =1,去分母后即可得出4ac-b2=4a,③正确;④根据抛物线的对称性可得出x=1与x=0时y值相等,由此可得出a+b+c=c>0,④错误.综上即可得出结论.
=1,去分母后即可得出4ac-b2=4a,③正确;④根据抛物线的对称性可得出x=1与x=0时y值相等,由此可得出a+b+c=c>0,④错误.综上即可得出结论.
①∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为x=-![]() =
=![]() ,
,
∴b=-a>0,
∵抛物线与y轴交点在y轴正半轴,
∴c>0,
∴abc<0,①正确;
②∵b=-a,
∴a+b=0,②正确;
③∵抛物线的顶点坐标为(![]() ,1),
,1),
∴![]() =1,
=1,
∴4ac-b2=4a,③正确;
④∵抛物线的对称轴为x=![]() ,
,
∴x=1与x=0时y值相等,
∵当x=0时,y=c>0,
∴当x=1时,y=a+b+c>0,④错误.
综上所述:正确的结论为①②③.
故选C.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
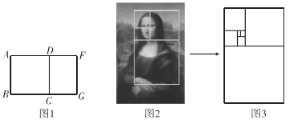
【题目】数学中,把长与宽之比为![]() (或宽与长之比为
(或宽与长之比为![]() )的矩形称为黄金矩形.
)的矩形称为黄金矩形.
思考解决下列问题:
(1)已知图1中黄金矩形![]() 的长
的长![]() ,求
,求![]() 的长;
的长;
(2)黄金矩形有个奇妙的特性:把图1中的黄金矩形![]() ,以
,以![]() 为边向矩形内作正方形
为边向矩形内作正方形![]() ,则矩形
,则矩形![]() 是否为黄金矩形,是,请予以证明;不是,请说明理由;
是否为黄金矩形,是,请予以证明;不是,请说明理由;
(3)黄金矩形使名画《蒙娜丽莎》显得特别和谐,专家分析画中布局如图2,其中最外面的矩形是黄金矩形,以黄金矩形的宽为边向矩形内部作正方形,由上小题知产生的小矩形为更小的黄金矩形,按此规律依次生成各黄金矩形,若图3中最大黄金矩形的长为![]() ,则最小黄金矩形的长是多少?
,则最小黄金矩形的长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小禾和小野按图示的规则玩“锤子”“剪刀”“布”游戏,游戏规则为:若一人出“剪刀”另一个出“布”,则出“剪刀”的胜;若一人出“锤子”另一个出“剪刀”,则出“锤子”的胜;若一人出“布”另一个出“锤子”,则出“布”的胜.若两人出相同的手势,则两人平局.
(1)用树状图或者表格表示小禾和小野玩一次所有可能的结果.

(2)这个游戏玩一次,小禾和小野分别胜出的概率是多少?从而说明游戏的公平性?
查看答案和解析>>
科目:初中数学 来源: 题型:
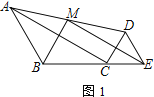
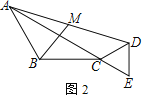
【题目】在△ABC中,AB=BC=![]() ,∠ABC=120°,△CDE为等边三角形,CD=2,连接AD,M为AD中点
,∠ABC=120°,△CDE为等边三角形,CD=2,连接AD,M为AD中点
(1)如图1,当B、C、E三点共线时,证明: BM⊥ME
(2)如图2,当A、C、E三点共线时,求BM的长
(3)如图3,取BE中点N,连MN.将△CDE绕点C旋转,直接写出旋转过程中线段MN的取值范围

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(0,2),B(p,q)在直线上,抛物线m经过点B、C(p+4,q),且它的顶点N在直线l上.
(1)若B(-2,1),
①请在平面直角坐标系中画出直线l与抛物线m的示意图;
②设抛物线m上的点Q的模坐标为e(-2≤e≤0)过点Q作x轴的垂线,与直线l交于点H.若QH=d,当d随e的增大面增大时,求e的取值范围;
(2)抛物线m与y轴交于点F,当抛物线m与x轴有唯一交点时,判断△NOF的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数y1=![]() 的图象经过点A,反比例函数y2=
的图象经过点A,反比例函数y2=![]() 的图象经过点B,则下列关于m,n的关系正确的是( )
的图象经过点B,则下列关于m,n的关系正确的是( )
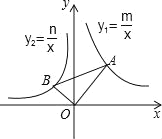
A.m=![]() nB.m=﹣
nB.m=﹣![]() nC.m=﹣
nC.m=﹣![]() nD.m=﹣3n
nD.m=﹣3n
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,点E是边AD的中点,连接BE并延长交CD的延长线于点F,交AC于点G.
(1)若FD=2, ![]() ,求线段DC的长;
,求线段DC的长;
(2)求证:EF·GB=BF·GE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 为常数)交
为常数)交![]() 轴于
轴于![]() 两点.
两点.
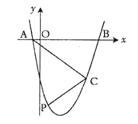
(1)求抛物线的解析式;
(2)直接写出:①抛物线的顶点坐标;
②抛物线与![]() 轴交点关于该抛物线对称轴对称的点
轴交点关于该抛物线对称轴对称的点![]() 的坐标;
的坐标;
(3)在直线![]() 下方的抛物线上是否存在点
下方的抛物线上是否存在点![]() 使
使![]() 的面积最大?若存在,请求出点
的面积最大?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com