练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列说法中，正确的是（ ）

    A.过一点有且只有一条直线与已知直线垂直

    B.过直线外一点有且只有一条直线与已知直线平行

    C.垂于同一条直线的两条直线平行

    D.如果两个角的两边分别平行，那么这两个角一定相等

    【答案】B

    【解析】

    根据平行线的性质和判定，平行线公理及推论逐个判断即可．

    A、在同一平面内，过一点有且只有一条直线与已知直线垂直，故本选项不符合题意；
    B、过直线外一点有且只有一条直线与已知直线平行，故本选项符合题意；
    C、在同一平面内，垂直于同一条直线的两直线平行，故本选项不符合题意；
    D、如果两个角的两边分别平行，那么这两个角相等或互补，故本选项不符合题意；
    故选：B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】线段AB的长为5，点A在平面直角坐标系中的坐标为（3，﹣2），点B的坐标为（3，x），则点B的坐标为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动，活动后，就活动的5个主题进行了抽样调查（每位同学只选最关注的一个），根据调查结果绘制了两幅不完整的统计图．根据图中提供的信息，解答下列问题：

    （1）这次调查的学生共有多少名？

    （2）请将条形统计图补充完整，并在扇形统计图中计算出“进取”所对应的圆心角的度数．

    （3）如果要在这5个主题中任选两个进行调查，根据（2）中调查结果，用树状图或列表法，求恰好选到学生关注最多的两个主题的概率（将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(8分)问题情景：某学校数学学习小组在讨论“随机掷二枚均匀的硬币，得到一正一反的概率是多少”时，小聪说：随机掷二枚均匀的硬币，可以有“二正、一正一反、二反”三种情况，所以，P（一正一反）＝；小颖反驳道：这里的“一正一反”实际上含有“一正一反，一反一正”二种情况，所以P（一正一反）＝.

    ⑴ 的说法是正确的.

    ⑵为验证二人的猜想是否正确，小聪与小颖各做了100次实验，得到如下数据：

    计算：小聪与小颖二人得到的“一正一反”的频率分别是多少？从他们的实验中，你能得

    到“一正一反”的概率是多少吗？

    ⑶对概率的研究而言小聪与小颖两位同学的实验说明了什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，O是坐标原点，点A的坐标是（﹣4，0），点B的坐标是（0，b）（b＞0），点P是直线AB上的一个动点，记点P关于y轴对称的点为P′．
    （1）当b=3时（如图1），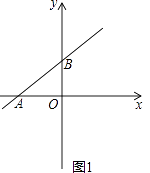

    ①求直线AB的函数表达式．
    （2）②在x轴上找一点Q（点O除外），使△APQ与△AOB全等，直接写出点Q的所有坐标
    （3）若点P在第一象限（如图2），设点P的横坐标为a，作PC⊥x轴于点C，连结AP′，CP′．当△ACP′是以点P′为直角顶点的等腰直角三角形时，求出a，b的值．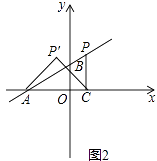

    （4）当线段OP′恰好被直线AB垂直平分时（如图3），直接写出b= ．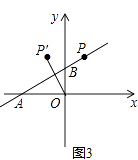

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，BO平分∠CBA，CO平分∠ACB，过O作EF∥BC，若AB＝12，AC＝8，求△AEF的周长。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB，CD交于点E，F，连接BF交AC于点M，连接DE，BO．若∠COB=60°，FO=FC，则下列结论：
    ①FB⊥OC，OM=CM；
    ②△EOB≌△CMB；
    ③四边形EBFD是菱形；
    ④MB：OE=3：2．
    其中正确结论的个数是（ ）
    A.1
    B.2
    C.3
    D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若5x﹣3y﹣2＝0，则25x÷23y﹣2＝_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，AD∥BC，AD=12cm，BC=15cm，点P自点A向D以1cm/s的速度运动，到D点即停止．点Q自点C向B以2cm/s的速度运动，到B点即停止，点P，Q同时出发，设运动时间为t（s）．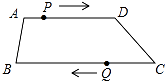
    （1）用含t的代数式表示： AP=；DP=；BQ=；CQ= ．
    （2）当t为何值时，四边形APQB是平行四边形？
    （3）当t为何值时，四边形PDCQ是平行四边形？

    查看答案和解析>>

    同步练习册答案