
【题目】如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论: 
①FB⊥OC,OM=CM;
②△EOB≌△CMB;
③四边形EBFD是菱形;
④MB:OE=3:2.
其中正确结论的个数是( )
A.1
B.2
C.3
D.4
【答案】C
【解析】解:连接BD,
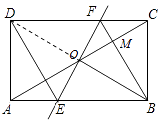
∵四边形ABCD是矩形,
∴AC=BD,AC、BD互相平分,
∵O为AC中点,
∴BD也过O点,
∴OB=OC,
∵∠COB=60°,OB=OC,
∴△OBC是等边三角形,
∴OB=BC=OC,∠OBC=60°,
在△OBF与△CBF中

∴△OBF≌△CBF(SSS),
∴△OBF与△CBF关于直线BF对称,
∴FB⊥OC,OM=CM;
∴①正确,
∵∠OBC=60°,
∴∠ABO=30°,
∵△OBF≌△CBF,
∴∠OBM=∠CBM=30°,
∴∠ABO=∠OBF,
∵AB∥CD,
∴∠OCF=∠OAE,
∵OA=OC,
易证△AOE≌△COF,
∴OE=OF,
∴OB⊥EF,
∴四边形EBFD是菱形,
∴③正确,
∵△EOB≌△FOB≌△FCB,
∴△EOB≌△CMB错误.
∴②错误,
∵∠OMB=∠BOF=90°,∠OBF=30°,
∴MB= ![]() ,OF=
,OF= ![]() ,
,
∵OE=OF,
∴MB:OE=3:2,
∴④正确;
故选:C.
【考点精析】利用矩形的性质对题目进行判断即可得到答案,需要熟知矩形的四个角都是直角,矩形的对角线相等.


 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】小强与小刚两位同学在学习“概率”时,做抛骰子(均匀立方体形状)试验,他们共抛了54次,出现不同向上点数的次数如下表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 6 | 9 | 5 | 8 | 16 | 10 |
(1)请计算出现向上点数为3的频率及出现向上点数为5的频率.
(2)小强说:“根据试验,一次试验中出现向上点数为5的概率最大.”小刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”请判断小强和小刚说法的对错.
(3)如果小强与小刚各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.过一点有且只有一条直线与已知直线垂直
B.过直线外一点有且只有一条直线与已知直线平行
C.垂于同一条直线的两条直线平行
D.如果两个角的两边分别平行,那么这两个角一定相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度,且点A、B、C均在格点上.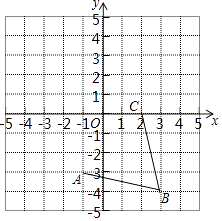
(1)请在所给的网格内画出以线段AB、BC为边的菱形并写出点D的坐标;
(2)菱形ABCD的周长为;
(3)菱形ABCD的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D、C在BF上,AC∥DE,∠A=∠E,BD=CF, 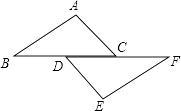
(1)求证:AB=EF.
(2)连接AF,BE,猜想四边形ABEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2008年5月12日14时28分四川汶川发生里氏8.0级强力地震.某市接到上级通知,立即派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题: 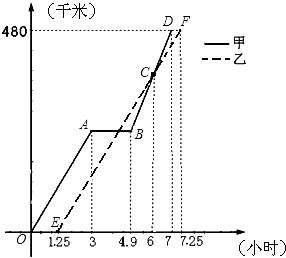
(1)由于汽车发生故障,甲组在途中停留了小时;
(2)甲组的汽车排除故障后,立即提速赶往灾区.请问甲组的汽车在排除故障时,距出发点的路程是多少千米?
(3)为了保证及时联络,甲、乙两组在第一次相遇时约定此后两车之间的路程不超过25千米,请通过计算说明,按图象所表示的走法是否符合约定?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com