
����Ŀ����֪������![]() �Ľ�xΪ��������yΪ����.
�Ľ�xΪ��������yΪ����.
��1����a��ȡֵ��Χ��
��2������Oa-3�O+�Oa+2�O��
��3�����̿���������д���������ǰѶ���ʽa2+2ab+b2��a2-2ab+b2������ȫƽ��ʽ�������һ������ʽ������ȫƽ��ʽ�����dz������±��Σ�������һ���ʵ����ʹʽ�г�����ȫƽ��ʽ���ټ�ȥ����ʹ����ʽ�ӵ�ֵ���䣬���ַ��������䷽�����䷽����һ����Ҫ�Ľ���������ѧ�������������Խ�һ�����Ʋ��ֽܷ�Ķ���ʽ�ֽ���ʽ�����ܽ��һЩ��Ǹ����йص�����������ʽ���ֵ����Сֵ�ȣ�
���磺�ֽ���ʽx2+2x-3=(x2+2x+1)-4=(x+1)2-4=(x+1)2-4=(x+1+2)(x+1-2)=(x+3)(x-1)��
�����Ķ��������䷽������������⣺
�ٷֽ���ʽ��m2-4m-5=
�ڵ�a��bΪ��ֵʱ������ʽa2+b2-4a+6b+13=0��
�۵�a��bΪ��ֵʱ������ʽa2-2ab+2b2-2a-4b+10=0��
���𰸡�(1) ![]() ����2��5����3����(m-5)(m+1)���ڵ�a=2��b=��3ʱ���۵�a=4��b=3ʱ,ԭʽ=0
����2��5����3����(m-5)(m+1)���ڵ�a=2��b=��3ʱ���۵�a=4��b=3ʱ,ԭʽ=0
��������
��1��ֱ����⣬�õ�����a�Ľ⣬Ȼ�������ɸ�����xΪ��������yΪ�������õ�����a��һԪһ�β���ʽ�飬����⼯����.
��2���ɣ�1��֪a�ķ�Χ�����жϳ�a-3��a+2����������ȥ����.
��3���ٸ���������䷽�����ص��m2��4m��5=m2��4m+4��9����ȥ������ȫƽ���ʽ.
�ڰ�ԭʽ�е�13��Ϊ![]() ���ٽ�ϳ�������ȫƽ��ʽ�����ڷǸ������������.
���ٽ�ϳ�������ȫƽ��ʽ�����ڷǸ������������.
�۰�ԭʼ��-2ab -2a��ϵõ�-2a��b+1����Ȼ����a2�䷽![]() �����������ʣ�µĵ���ʽ�õ���һ����ȫƽ��ʽ��������.
�����������ʣ�µĵ���ʽ�õ���һ����ȫƽ��ʽ��������.
(1)�ⷽ����![]() ��
��![]() �����⣬��
�����⣬��![]() ���
���![]() .
.
(2)��![]() ����
����![]() ��
��![]()
��![]() =3-a+��a+2��=5
=3-a+��a+2��=5
(3)
��m2��4m��5=m2��4m+4��9=��m��2��2��9 =��m��2+3����m��2��3��
=��m+1����m��5����
�ڡ�a2+b2��4a+6b+13=��a��2��2+��b+3��2��
�൱a=2��b=��3ʱ,ԭʽΪ0.
�ۡ�a2��2ab+2b2��2a��4b+10=0
��![]()

��![]()
��![]() ʱ��ԭʽΪ0.
ʱ��ԭʽΪ0.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͨ��ѧϰ���Ǻ���������֪����ֱ���������У�һ����ǵĴ�С�������߳��ı�ֵ�Ψһȷ������˱߳���ǵĴ�С֮������ת��.���Ƶģ������ڵ����������н����߽�֮�����ϵ.���Ƕ��壺�����������еױ������ıȽ������ǵ�����(sad).��ͼ1���ڡ�ABC�У�AB��AC������A�����Լ���sadA����ʱsadA��![]() .����֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ����.���������ǵ����Զ��壬����������⣺
.����֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ����.���������ǵ����Զ��壬����������⣺

(1)sad60�㣽 ��
(2)����0�㣼��A��180�㣬��A������ֵsadA��ȡֵ��Χ�� ��
(3)��ͼ�ڣ���֪sinA��![]() �����С�AΪ��ǣ�����sadA��ֵ.
�����С�AΪ��ǣ�����sadA��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��������ABCD�У�AB��CD����D=90�㣬AD=CD=2����E�ڱ�AD�ϣ������A��D�غϣ�����CEB=45�㣬EB��Խ���AC�ཻ�ڵ�F����DE=x��
��1���ú�x�Ĵ���ʽ��ʾ�߶�CF�ij���
��2���������CAE���ܳ�����C��CAE����BAF���ܳ�����C��BAF����![]() =y����y����x�ĺ�����ϵʽ����д�����Ķ�����
=y����y����x�ĺ�����ϵʽ����д�����Ķ�����
��3������ABE������ֵ��![]() ʱ����AB�ij���
ʱ����AB�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a��b��������������ʵ�������ǹ涨�����㲻��ʽa��x��b��ʵ��x������ȡֵ��ȫ����������䣬��ʾΪ[a��b]������һ����������������Ա���x�뺯��ֵy���㣺��m��x��nʱ����m��y��n�����Ǿͳƴ˺����DZ�����[m��n]�ϵġ��պ��������纯��y=��x+4����x=1ʱ��y=3����x=3ʱ��y=1������1��x��3ʱ������1��y��3������˵����y=��x+4�DZ�����[1��3]�ϵġ��պ�������ͬ������y=xҲ�DZ�����[1��3]�ϵġ��պ�������
��1������������y=![]() �DZ�����[1��2018]�ϵġ��պ����������жϲ�˵�����ɣ�
�DZ�����[1��2018]�ϵġ��պ����������жϲ�˵�����ɣ�
��2�������֪���κ���y=x2��4x+k�DZ�����[2��t]�ϵġ��պ���������k��t��ֵ��
��3�������2�������Ķ��κ�����ͼ��y����C�㣬AΪ�˶��κ���ͼ��Ķ��㣬BΪֱ��x=1�ϵ�һ�㣬����ABCΪֱ��������ʱ��д����B�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ι��ţ�����������ˮ��2mʱ��ˮ���4m��ˮ���½�2.5m��ˮ��������ӣ�������

A. 1 m B. 2 m C. 3 m D. 6 m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC��D��BC������һ�㣬��D�ֱ���AB��AC�����ߣ�����ֱ�ΪE��F��CG��AB���ϵĸߣ�
��1����D����BC��ʲôλ��ʱ��DE=DF����˵�����ɣ�
��2��DE��DF��CG�ij�֮������������ĵ�����ϵ����˵������.
��3����D�ڵױ�BC���ӳ����ϣ���2���еĽ��ۻ������������������ִ��������Ĺ�ϵ����˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����12�֣���ͼ��ʾ�������Ľ����������ߺͳ����ι��ɣ������εij���12 m������4 m������ͼ����ʾ��ֱ������ϵ�������߿�����y=![]() x2+bx+c��ʾ�����������ϵĵ�C��OB��ˮƽ����Ϊ3 m��������OA�ľ���Ϊ
x2+bx+c��ʾ�����������ϵĵ�C��OB��ˮƽ����Ϊ3 m��������OA�ľ���Ϊ![]() m.
m.
��1���������ߵĺ�����ϵʽ�������������D������OA�ľ��룻
��2��һ������������һ�����弯װ����Ϊ6m����Ϊ4m�������������˫������ô���������ܷ�ȫͨ����
��3������������������Ҫ��װ���ŵƣ�ʹ���������ĸ߶���ȣ�����������ĸ߶Ȳ�����8m����ô���ŵƵ�ˮƽ������С�Ƕ����ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ABC=45�� �� BC=4����ACΪֱ�DZߣ���AΪֱ�Ƕ������ABC�����������ֱ��������ACD������BD�����DBC�����Ϊ( ) .
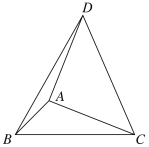
A.8B.10C.4![]() D.8
D.8![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���A�á�B�á�C=3��5��10������MNC�ա�ABC�����BCM�á�BCN���ڣ� ��

A. 1��2 B. 1��3 C. 2��3 D. 1��4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com