
����Ŀ��ͨ��ѧϰ���Ǻ���������֪����ֱ���������У�һ����ǵĴ�С�������߳��ı�ֵ�Ψһȷ������˱߳���ǵĴ�С֮������ת��.���Ƶģ������ڵ����������н����߽�֮�����ϵ.���Ƕ��壺�����������еױ������ıȽ������ǵ�����(sad).��ͼ1���ڡ�ABC�У�AB��AC������A�����Լ���sadA����ʱsadA��![]() .����֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ����.���������ǵ����Զ��壬����������⣺
.����֪��һ���ǵĴ�С������ǵ�����ֵҲ���Ψһȷ����.���������ǵ����Զ��壬����������⣺

(1)sad60�㣽 ��
(2)����0�㣼��A��180�㣬��A������ֵsadA��ȡֵ��Χ�� ��
(3)��ͼ�ڣ���֪sinA��![]() �����С�AΪ��ǣ�����sadA��ֵ.
�����С�AΪ��ǣ�����sadA��ֵ.
���𰸡�(1)1;(2) 0<sadA<2; (3) ![]() .
.
��������
��1���������⣬�ж�������Ϊ�ȱ������Σ�Ȼ��������ԵĶ�����
��2�����0���180��ʱ���������ε����ıȼ��ɣ�
��3����ͼ����AB��ȡAD��AC������D��DE��AC�ڵ�E������CD����AB��5a��BC��3a����AC��4a��Ȼ�����CD�ij����ٸ������ԵĶ�����.
�⣺(1)���������֪��������Ϊ60��ʱ�����������ε�ҲΪ60�㣬
���������Ϊ�ȱ������Σ�
��sad60�㣽1��
�ʴ�Ϊ1��
(2)����A�ӽ�0��ʱ��sadA�ӽ�0��
����A�ӽ�180��ʱ�����������εĵӽ������Ķ�������sadA�ӽ�2��
��sadA��ȡֵ��ΧΪ��0<sadA<2��
(3) 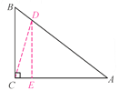 ��AB��5a��BC��3a����AC��4a��
��AB��5a��BC��3a����AC��4a��
��ͼ����AB��ȡAD��AC��4a������D��DE��AC�ڵ�E������CD��
��DE��AD��sinA��4a��![]() ��
��![]() a��AE��AD��cosA��4a��
a��AE��AD��cosA��4a��![]() ��
��![]() a��
a��
��CE��4a��![]() a��
a��![]() a��
a��
����Rt��DCE��
CD��![]() ��
��![]() ��
��![]() a��
a��
��sadA��![]() ��
��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���������κ��ĸ�ȫ�ȵ�С�����ΰ�ͼ�١������ַ�ʽ�ڷţ���С�����εı߳�Ϊx������ϸ�۲�ͼ�λش��������⣮
��1���ú�a��b�Ĵ���ʽ��ʾx����x���� ����
��2���ú�a��b�Ĵ���ʽ��ʾ�������εı߳��� �������뽫�����Ϊ���
��3������ǰ���ʵĽ������ͼ�ڵĴ���������δ��С�����θ��Dz��ֵ����������a��b�Ĵ���ʽ��ʾ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ����CD�С�O�ڵ�C����BA���ӳ��߽��ڵ�D��OE��AB����O�ڵ�E������CA��CE��CB��CE��AB�ڵ�G������A��AF��CE�ڵ�F���ӳ�AF��BC�ڵ�P��
���������CPA�Ķ�����
����������OF����AC=![]() ����D=30�������߶�OF�ij���
����D=30�������߶�OF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪˫����y��![]() (k��0)��ͼ��Rt��OAB��б��OB���е�D����ֱ�DZ�AB�ཻ�ڵ�C.��BC��OA��6ʱ��k��___��
(k��0)��ͼ��Rt��OAB��б��OB���е�D����ֱ�DZ�AB�ཻ�ڵ�C.��BC��OA��6ʱ��k��___��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�س���Ʒѷ�����ͼ��x��km����ʾ��ʻ��̣�y��Ԫ����ʾ���ѣ������ͼ�����������⣺
��1���õس�������� Ԫ��
��2����x��2ʱ����y��x֮��ĺ�����ϵʽ��
��3����ij�˿���һ�γ˳�������Ϊ18km������λ�˿��踶������Ѷ���Ԫ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��a��0����ͼ���һ���֣������ߵĶ���������A��1��4������x���һ��������B��3��0�������н��ۣ���abc��0����2a+b=0���۷���ax2+bx+c=4��������ȵ�ʵ����������������x�����һ�������ǣ���2.0������x��ax+b����a+b��������ȷ���۵ĸ����ǣ�������

A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB��CD����ABK�Ľ�ƽ����BE�ķ����ӳ��ߺ���DCK�Ľ�ƽ����CF�ķ����ӳ��߽��ڵ�H����K����H=27��������K=��������

A. 76�� B. 78�� C. 80�� D. 82��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �Ľ�xΪ��������yΪ����.
�Ľ�xΪ��������yΪ����.
��1����a��ȡֵ��Χ��
��2������Oa-3�O+�Oa+2�O��
��3�����̿���������д���������ǰѶ���ʽa2+2ab+b2��a2-2ab+b2������ȫƽ��ʽ�������һ������ʽ������ȫƽ��ʽ�����dz������±��Σ�������һ���ʵ����ʹʽ�г�����ȫƽ��ʽ���ټ�ȥ����ʹ����ʽ�ӵ�ֵ���䣬���ַ��������䷽�����䷽����һ����Ҫ�Ľ���������ѧ�������������Խ�һ�����Ʋ��ֽܷ�Ķ���ʽ�ֽ���ʽ�����ܽ��һЩ��Ǹ����йص�����������ʽ���ֵ����Сֵ�ȣ�
���磺�ֽ���ʽx2+2x-3=(x2+2x+1)-4=(x+1)2-4=(x+1)2-4=(x+1+2)(x+1-2)=(x+3)(x-1)��
�����Ķ��������䷽������������⣺
�ٷֽ���ʽ��m2-4m-5=
�ڵ�a��bΪ��ֵʱ������ʽa2+b2-4a+6b+13=0��
�۵�a��bΪ��ֵʱ������ʽa2-2ab+2b2-2a-4b+10=0��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com