
【题目】如图,在ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=3,EF=1,则BC长为( ) 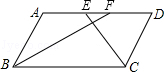
A.4
B.5
C.6
D.7
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】为了响应“足球进校园”的目标,某校计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元. 
(1)求A,B两种品牌的足球的单价.
(2)求该校购买20个A品牌的足球和2个B品牌的足球的总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班学生在颁奖大会上得知该班获得奖励的情况如下表:
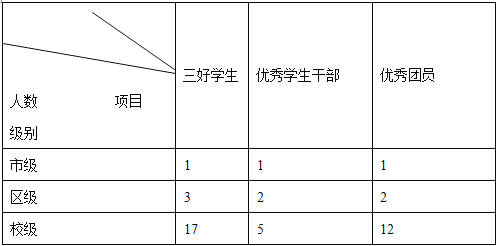
已知该班共有27人获得奖励(每位同学均可获得不同级别、不同类别多项奖励),其中只获得两项奖励的有13人,那么该班获得奖励最多的一位同学可能获得的奖励为( )
A. 3项 B. 4项 C. 5项 D. 6项
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点A向右移动1个单位得到点B,点B向右移动(n+1)(n为正整数)个单位得到点C,点A、B、C分别表示有理数a、b、c.
(1)当n=1时,A、B、C三点在数轴上的位置如图所示,a、b、c三个数的乘积为正数.
![]()
①数轴上原点的位置可能( )
A.在点A左侧或在A、B两点之间
B.在点C右侧或在A、B两点之间
C.在点A左侧或在B、C两点之间
D.在点C右侧或在B、C两点之间
②若这三个数的和与其中的一个数相等,则a=_________(简述理由)
(2)将点C向右移动(n+2)个单位得到点D,点D表示有理数d,a、b、c、d四个数的积为正数,且这四个数的和与其中的两个数的和相等,a为整数,若n分别取1,2,3,…,100时,对应的a的值分别记为![]() ,…,
,…,![]() ,则
,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该企业招收了新工人,设新工人李明第x天生产的粽子数量为y只,y与x满足下列关系式: y= ![]() .
.
(1)李明第几天生产的粽子数量为420只?
(2)如图,设第x天每只粽子的成本是p元,p与x之间的关系可用图中的函数图象来刻画.若李明第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价﹣成本) 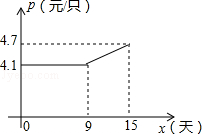
(3)设(2)小题中第m天利润达到最大值,若要使第(m+1)天的利润比第m天的利润至少多48元,则第(m+1)天每只粽子至少应提价几元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AC和AB上的点,BD与CE相交于点O,给出下列四个条件:
①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD;④OB=OC.

(1)上述四个条件中,由哪两个条件可以判定AB=AC?(用序号写出所有的情形)
(2)选择(1)小题中的一种情形,说明AB=AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C、D是线段AB上两点,已知AC:CD:DB=1:2:3,M、N分别为AC、DB的中点,且AB=12cm,
(1)求线段CD的长;
(2)求线段MN的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为正方形ABCD的中心,M为射线OD上一动点(M与点O,D不重合),以线段AM为一边作正方形AMEF,连接FD.
(1)当点M在线段OD上时(如图1),线段BM与DF有怎样的数量及位置关系?请说明理由;
(2)当点M在线段OD的延长线上时(如图2),(1)中的结论是否仍然成立?请结合图2说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①单项式-![]() 的系数为-
的系数为-![]() ,次数为2;②90°的角叫余角,180°的角叫补角③若AC=BC,则点C是线段AB的中点;④经过一点有且只有一条直线与这条直线平行,其中错误的说法有( )
,次数为2;②90°的角叫余角,180°的角叫补角③若AC=BC,则点C是线段AB的中点;④经过一点有且只有一条直线与这条直线平行,其中错误的说法有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com