
【题目】如图,已知∠ABC=90°,D是直线AB上的点,AD=BC.
(1)如图1,过点A作AF⊥AB,截取AF=BD,连接DC、DF、CF,判断△CDF的形状并证明;
(2)如图2,E是直线BC上一点,且CE=BD,直线AE、CD相交于点P,∠APD的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由.

【答案】(1)△CDF是等腰三角形;(2)∠APD=45°.
【解析】试题分析:(1)利用SAS证明△AFD和△BDC全等,再利用全等三角形的性质得出FD=DC,即可判断三角形的形状;
(2)作AF⊥AB于A,使AF=BD,连结DF,CF,利用SAS证明△AFD和△BDC全等,再利用全等三角形的性质得出FD=DC,∠FDC=90°,即可得出∠FCD=∠APD=45°.
试题解析:(1)△CDF是等腰直角三角形,理由如下:
∵AF⊥AD,∠ABC=90°,∴∠FAD=∠DBC,
在△FAD与△DBC中, 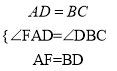 ,∴△FAD≌△DBC(SAS),
,∴△FAD≌△DBC(SAS),
∴FD=DC,∴△CDF是等腰三角形,∵△FAD≌△DBC,∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,∴∠BDC+∠FDA=90°,
∴△CDF是等腰直角三角形;
(2)作AF⊥AB于A,使AF=BD,连结DF,CF,如图,∵AF⊥AD,∠ABC=90°,
∴∠FAD=∠DBC,在△FAD与△DBC中, 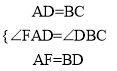 ,∴△FAD≌△DBC(SAS),
,∴△FAD≌△DBC(SAS),
∴FD=DC,∴△CDF是等腰三角形,∵△FAD≌△DBC,∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,∴∠BDC+∠FDA=90°,∴△CDF是等腰直角三角形,
∴∠FCD=45°,∵AF∥CE,且AF=CE,∴四边形AFCE是平行四边形,
∴AE∥CF,∴∠APD=∠FCD=45°.



科目:初中数学 来源: 题型:
【题目】某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示.

(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个数的加上(或减去)这两个数的,这样的多项式叫做完全平方式;其特征是:
①多项式是项式;
②经升(降)幂排列后,首尾两项是且同号;中间项除符号外是首尾两项的积的2倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列对于式子﹣(﹣5)的解释:
①可以表示﹣5的相反数;
②可以表示﹣1与﹣5的积;
③结果等于﹣5的绝对值.
其中表述错误的个数为( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com