
【题目】(2016四川省乐山市第22题)“六一”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:

(1)小张如何进货,使进货款恰好为1300元?
(2)要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮小张设计一个进货方案,并求出其所获利润的最大值.
【答案】(1)A文具为40只,B文具60只;(2)各进50只,最大利润为500元.
【解析】
试题分析:(1)设A文具为x只,则B文具为(100﹣x)只,根据题意列出方程解答即可;
(2)设A文具为x只,则B文具为(100﹣x)只,根据题意列出函数解答即可.
试题解析:(1)设A文具为x只,则B文具为(100﹣x)只,可得:10x+15(100﹣x)=1300,解得:x=40.
答:A文具为40只,则B文具为100﹣40=60只;
(2)设A文具为x只,则B文具为(100﹣x)只,可得:
(12﹣10)x+(23﹣15)(100﹣x)≤40%[10x+15(100﹣x)],解得:x≥50,
设利润为y,则可得:y=(12﹣10)x+(23﹣15)(100﹣x)=2x+800﹣8x=﹣6x+800,
因为是减函数,所以当x=50时,利润最大,即最大利润=﹣50×6+800=500元.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
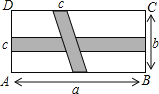
【题目】如图,在长方形ABCD中,横向阴影部分是长方形,另一阴影部分是平行四边形,根据图中标注的数据.
(1)用式子表示图中空白部分的面积;
(2)当a=50,b=30,c=4时,空白部分的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;
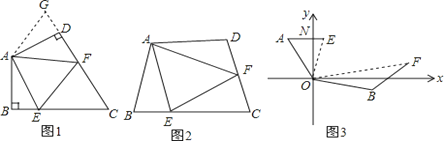
(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,CD上的点,且∠EAF=![]() ∠BAD上述结论是否仍然成立,并说明理由;
∠BAD上述结论是否仍然成立,并说明理由;
(3)如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016浙江省舟山市第19题)太阳能光伏建筑是现代绿色环保建筑之一,老张准备把自家屋顶改建成光伏瓦面,改建前屋顶截面△ABC如图2所示,BC=10米,∠ABC=∠ACB=36°,改建后顶点D在BA的延长线上,且∠BDC=90°,求改建后南屋面边沿增加部分AD的长.(结果精确到0.1米)
(参考数据:sin18°≈0.31,cos18°≈0.95.tan18°≈0.32,sin36°≈0.59.cos36°≈0.81,tan36°≈0.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
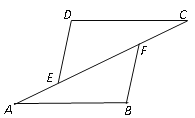
【题目】如图6,已知A、E、F、C四点共线,BF=DE,AB=CD.
(1)请你添加一个条件(不再添加其它线段,不再标注或使用其他字母),使△DEC ≌△BFA,并给出证明.你添加的条件是:_______________;
(2)在(1)的基础上,求证:DE∥BF。
查看答案和解析>>
科目:初中数学 来源: 题型:
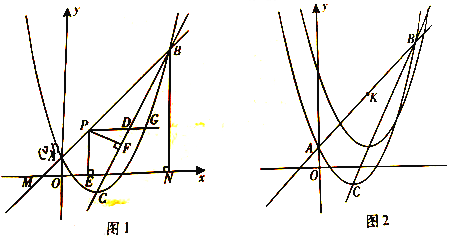
【题目】(2016重庆市第26题)如图1,二次函数![]() 的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作x轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.
的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作x轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.
(1)求直线AB和直线BC的解析式;
(2)点P是线段AB上一点,点D是线段BC上一点,PD//x轴,射线PD与抛物线交于点G,过点P作PE⊥x轴于点E,PF⊥BC于点F,当PF与PE的乘积最大时,在线段AB上找一点H(不与点A,点B重合),使GH+![]() BH的值最小,求点H的坐标和GH+
BH的值最小,求点H的坐标和GH+![]() BH的最小值;
BH的最小值;
(3)如图2,直线AB上有一点K(3,4),将二次函数![]() 沿直线BC平移,平移的距离是t(t≥0),平移后抛物线使点A,点C的对应点分别为点A’,点C’;当△A’C’K是直角三角形时,求t的值。
沿直线BC平移,平移的距离是t(t≥0),平移后抛物线使点A,点C的对应点分别为点A’,点C’;当△A’C’K是直角三角形时,求t的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com