
【题目】写出命题“等腰三角形底边上的高线与顶角平分线重合”的逆命题,这个逆命题是真命题吗?请证明你的结论
【答案】逆命题:有一条边上的高线和这条边的对角平分线重合的三角形是等腰三角形,为真命题,证明见解析.
【解析】试题分析:根据逆命题的相关知识可将命题的题设和结论交换位置得到逆命题,然后利用三角形全等的判定和性质进行证明即可.
试题解析:逆命题:有一条边上的高线和这条边的对角平分线重合的三角形是等腰三角形
这个命题是真命题.
已知:如图,在△ABC中,AD⊥BC,且AD平分∠BAC.求证:三角形ABC是等腰三角形
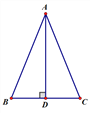
证明:∵AD⊥BC
∴ ∠BDA=∠CDA,
∵AD平分∠BA,
∴∠DAB=∠DAC,
在△ABD和△ACD中,
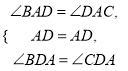
∴△ABD≌△ACD(ASA)
∴AB=AC,
∴△ABC是等腰三角形.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】(2016广西省贺州市第24题)某地区2014年投入教育经费2900万元,2016年投入教育经费3509万元.
(1)求2014年至2016年该地区投入教育经费的年平均增长率;
(2)按照义务教育法规定,教育经费的投入不低于国民生产总值的百分之四,结合该地区国民生产总值的增长情况,该地区到2018年需投入教育经费4250万元,如果按(1)中教育经费投入的增长率,到2018年该地区投入的教育经费是否能达到4250万元?请说明理由.
(参考数据:![]() =1.1,
=1.1,![]() =1.2,
=1.2,![]() =1.3,
=1.3,![]() =1.4)
=1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016四川省乐山市第22题)“六一”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:

(1)小张如何进货,使进货款恰好为1300元?
(2)要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮小张设计一个进货方案,并求出其所获利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
①两个无理数的和一定是无理数;
②两个无理数的积一定是无理数;
③一个有理数与一个无理数的和一定是无理数;
④一个有理数与一个无理数的积一定是无理数。其中正确的个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知实数x,y满足|x﹣4|+(y﹣8)2=0,则以x,y的值为两边长的等腰三角形的周长是( )
A.20或16B.20C.16D.以上答案均不对
查看答案和解析>>
科目:初中数学 来源: 题型:
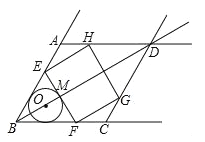
【题目】(2016浙江省温州市第24题)如图,在射线BA,BC,AD,CD围成的菱形ABCD中,∠ABC=60°,AB=6![]() ,O是射线BD上一点,⊙O与BA,BC都相切,与BO的延长线交于点M.过M作EF⊥BD交线段BA(或射线AD)于点E,交线段BC(或射线CD)于点F.以EF为边作矩形EFGH,点G,H分别在围成菱形的另外两条射线上.
,O是射线BD上一点,⊙O与BA,BC都相切,与BO的延长线交于点M.过M作EF⊥BD交线段BA(或射线AD)于点E,交线段BC(或射线CD)于点F.以EF为边作矩形EFGH,点G,H分别在围成菱形的另外两条射线上.
(1)求证:BO=2OM.
(2)设EF>HE,当矩形EFGH的面积为24![]() 时,求⊙O的半径.
时,求⊙O的半径.
(3)当HE或HG与⊙O相切时,求出所有满足条件的BO的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com