
分析 根据题意大致画出二次函数的图象,如图,利用函数图象可对①②③④直接判断;根据二次函数的性质对⑤进行判断.
解答 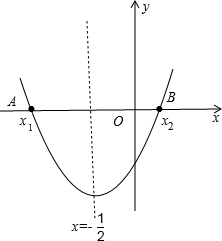 解:如图,当点P(m,n)在第四象限内的抛物线上时,n<0,而m>0,所以①错误;
解:如图,当点P(m,n)在第四象限内的抛物线上时,n<0,而m>0,所以①错误;
当m>x2时,点P(m,n)在x轴上方,则n>0,所以②正确;
当n<0时,点P(m,n)在x轴下方,则x1<m<x2,所以③正确;
当n>0时,x<x1或x>x2,所以④错误;
抛物线的对称轴为直线x=-$\frac{1}{2}$,所以当m$<-\frac{1}{2}$时,n随着m的增大而减小,所以⑤正确.
故答案为②③⑤.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.也考查了二次函数的性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
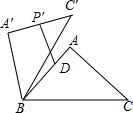 如图,将锐角△ABC绕点B逆时针旋转α(其中0°<α≤360°),得到△A′BC′,点D是边AB的中点,点P是边AC(含端点)上的一个动点,在△ABC绕点B逆时针旋转的过程中,点P的对应点是点P′.若AB=10,AC=8$\sqrt{2}$,∠ACB=45°,DP′的长度为x,则x的取值范围是7$\sqrt{2}$-5≤x≤19.
如图,将锐角△ABC绕点B逆时针旋转α(其中0°<α≤360°),得到△A′BC′,点D是边AB的中点,点P是边AC(含端点)上的一个动点,在△ABC绕点B逆时针旋转的过程中,点P的对应点是点P′.若AB=10,AC=8$\sqrt{2}$,∠ACB=45°,DP′的长度为x,则x的取值范围是7$\sqrt{2}$-5≤x≤19.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
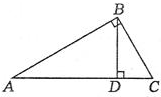 如图,Rt△ABC中,∠ABC=90°,BD⊥AC,BC=5,BD=4,则S△BCD:S△ABD=9:16,cos∠ABD=$\frac{3}{5}$,AB=$\frac{20}{3}$.
如图,Rt△ABC中,∠ABC=90°,BD⊥AC,BC=5,BD=4,则S△BCD:S△ABD=9:16,cos∠ABD=$\frac{3}{5}$,AB=$\frac{20}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
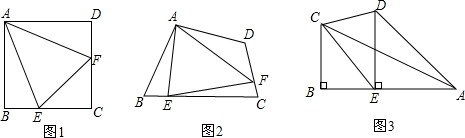
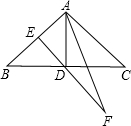 在学习了三角形的相关知识后,老师给小梅留了道作业题,请你帮小梅做完这道题.
在学习了三角形的相关知识后,老师给小梅留了道作业题,请你帮小梅做完这道题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com