
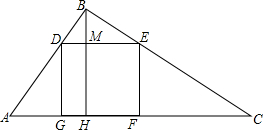
 如图,有一块直角三角形木板ABC,面积为1.5m2,一条直角边AB为1.5m,现在要把它按图示加工成一个正方形桌面DEFG.
如图,有一块直角三角形木板ABC,面积为1.5m2,一条直角边AB为1.5m,现在要把它按图示加工成一个正方形桌面DEFG.分析 (1)根据三角形的面积公式得到等积式,求得BH的长度;
(2)由DE∥AC,得到△BDE∽△BAC,证得比例式$\frac{BM}{BH}=\frac{DE}{AC}$,代入有关数据即可得到结果.
解答 解:(1)∵AB=1.5m,S△ABC=1.5m2,∠ACB=90°,
∴BC=2m,AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=2.5m,
∵S△ABC=$\frac{1}{2}$AC•BH=$\frac{1}{2}$AB•BC,
∴BH=$\frac{AB•BC}{AC}$=$\frac{1.5×2}{2.5}$=$\frac{6}{5}$;
(2)设正方形的边长为x,
∵DE∥AC,
∴△BDE∽△BAC,
∴$\frac{BM}{BH}=\frac{DE}{AC}$,
即$\frac{\frac{6}{5}-x}{\frac{6}{5}}$=$\frac{x}{2.5}$,
解得:x=$\frac{30}{37}$,
∴正方形DEFG的边长为$\frac{30}{37}$.
点评 本题考查了相似三角形的判定和性质,正方形的性质,勾股定理,三角形的面积,熟练掌握各定理是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
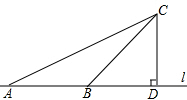 如图,某公路稽查站设立了如下测速方法:先在公路旁选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于21m,∠ACD=60°,∠BCD=30°.某辆汽车从A到B用时为2s,本路段对汽车限速为40km/h,这辆汽车是否超速?说明理由.($\sqrt{3}$≈1.732)
如图,某公路稽查站设立了如下测速方法:先在公路旁选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于21m,∠ACD=60°,∠BCD=30°.某辆汽车从A到B用时为2s,本路段对汽车限速为40km/h,这辆汽车是否超速?说明理由.($\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
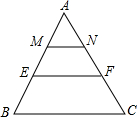 如图,在△ABC中,M,E把AB边三等分,MN∥EF∥BC,则△AMN,四边形MEFN,四边形EBCF的面积比为( )
如图,在△ABC中,M,E把AB边三等分,MN∥EF∥BC,则△AMN,四边形MEFN,四边形EBCF的面积比为( )| A. | 1:1:1 | B. | 1:2:3 | C. | 1:4:9 | D. | 1:3:5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
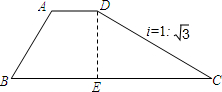 如图,梯形ABCD是拦水坝的横断面图,图中斜坡CD的坡度i=1:$\sqrt{3}$,∠B=60°,AB=6,AD=4,拦水坝的横断面ABCD的面积30$\sqrt{3}$.
如图,梯形ABCD是拦水坝的横断面图,图中斜坡CD的坡度i=1:$\sqrt{3}$,∠B=60°,AB=6,AD=4,拦水坝的横断面ABCD的面积30$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{12}$ | B. | $\sqrt{18}$ | C. | $\root{3}{2}$ | D. | $\sqrt{20}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com