
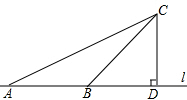
 如图,某公路稽查站设立了如下测速方法:先在公路旁选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于21m,∠ACD=60°,∠BCD=30°.某辆汽车从A到B用时为2s,本路段对汽车限速为40km/h,这辆汽车是否超速?说明理由.($\sqrt{3}$≈1.732)
如图,某公路稽查站设立了如下测速方法:先在公路旁选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于21m,∠ACD=60°,∠BCD=30°.某辆汽车从A到B用时为2s,本路段对汽车限速为40km/h,这辆汽车是否超速?说明理由.($\sqrt{3}$≈1.732) 分析 分别在Rt△ADC和Rt△BCD中,求得AB的长,由从A到B用时2秒,即可求得这辆校车的速度,比较与40千米/小时的大小,即可确定这辆校车是否超速.
解答  解:超速.
解:超速.
理由:由題意得,
在Rt△ADC和Rt△BCD中,∠ACD=60°,∠BCD=30°,
∠CAD=∠ACB=30°,
故AB=BC,
在Rt△BDC中,cos30°=$\frac{CD}{BC}$=$\frac{21}{BC}$=$\frac{\sqrt{3}}{2}$,
则AB=BC=14$\sqrt{3}$≈24.2(米),
∵汽车从A到B用时2秒,
∴速度为24.2÷2=12.1(米/秒),
∵12.1×3600=43560(米/时),
∴该车速度为43.56千米/小时,
∵大于40千米/小时,
∴此校车在AB路段超速.
点评 此题考查了解直角三角形的应用问题.此题难度适中,解题的关键是把实际问题转化为数学问题求解,注意数形结合思想的应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
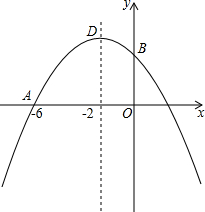 已知抛物线y=ax2-x+c过点A(-6,0),对称轴是直线x=-2,与y轴交于点B,顶点为D.
已知抛物线y=ax2-x+c过点A(-6,0),对称轴是直线x=-2,与y轴交于点B,顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
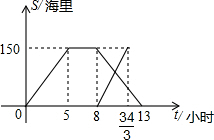 黄岩岛是我国南沙群岛的一个小岛,一天某渔船在该海域捕鱼,突然发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告并立即返航,渔政船接到报告后,立即出发赶往黄岩岛.下图是渔政船及渔船与港口的距离s和渔船离开港口的时间t的函数图象.(假设渔船和渔政船沿同一航线航行)则在渔政船驶往黄岩岛的过程中,渔船从港口出发经过9.6或10.4小时与渔政船相距30海里.
黄岩岛是我国南沙群岛的一个小岛,一天某渔船在该海域捕鱼,突然发现一外国舰艇进入我国水域向黄岩岛驶来,渔船向渔政部门报告并立即返航,渔政船接到报告后,立即出发赶往黄岩岛.下图是渔政船及渔船与港口的距离s和渔船离开港口的时间t的函数图象.(假设渔船和渔政船沿同一航线航行)则在渔政船驶往黄岩岛的过程中,渔船从港口出发经过9.6或10.4小时与渔政船相距30海里.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
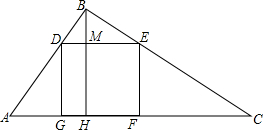 如图,有一块直角三角形木板ABC,面积为1.5m2,一条直角边AB为1.5m,现在要把它按图示加工成一个正方形桌面DEFG.
如图,有一块直角三角形木板ABC,面积为1.5m2,一条直角边AB为1.5m,现在要把它按图示加工成一个正方形桌面DEFG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com