
(11分)(2013•抚顺)在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,DE⊥BC,垂足为点E,连接CD.
(1)如图1,DE与BC的数量关系是 _________ ;
(2)如图2,若P是线段CB上一动点(点P不与点B、C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连接BF,请猜想DE、BF、BP三者之间的数量关系,并证明你的结论;
(3)若点P是线段CB延长线上一动点,按照(2)中的作法,请在图3中补全图形,并直接写出DE、BF、BP三者之间的数量关系.

(1)DE= BC;
BC;
(2)BF+BP= DE;
DE;
(3)BF﹣BP= DE.
DE.
【解析】
试题分析:(1)由∠ACB=90°,∠A=30°得到∠B=60°,根据直角三角形斜边上中线性质得到DB=DC,则可判断△DCB为等边三角形,由于DE⊥BC,DE= BC;
BC;
(2)根据旋转的性质得到∠PDF=60°,DP=DF,易得∠CDP=∠BDF,则可根据“SAS”可判断△DCP≌△DBF,则CP=BF,利用CP=BC﹣BP,DE= BC可得到BF+BP=
BC可得到BF+BP= DE;
DE;
(3)与(2)的证明方法一样得到△DCP≌△DBF得到CP=BF,而CP=BC+BP,则BF﹣BP=BC,所以BF﹣BP= DE.
DE.
试题解析:(1)∵∠ACB=90°,∠A=30°,
∴∠B=60°,
∵点D是AB的中点,
∴DB=DC,
∴△DCB为等边三角形,
∵DE⊥BC,
∴DE= BC;
BC;
故答案为DE= BC.
BC.
(2)BF+BP= DE.理由如下:
DE.理由如下:
∵线段DP绕点D逆时针旋转60°,得到线段DF,
∴∠PDF=60°,DP=DF,
而∠CDB=60°,
∴∠CDB﹣∠PDB=∠PDF﹣∠PDB,
∴∠CDP=∠BDF,
在△DCP和△DBF中
DC=DB,∠CDP=∠BDF,DP=DF,
∴△DCP≌△DBF(SAS),
∴CP=BF,
而CP=BC﹣BP,
∴BF+BP=BC,
∵DE= BC,
BC,
∴BC= DE,
DE,
∴BF+BP= DE;
DE;
(3)如图,

与(2)一样可证明△DCP≌△DBF,
∴CP=BF,
而CP=BC+BP,
∴BF﹣BP=BC,
∴BF﹣BP= DE.
DE.
考点:1.全等三角形的判定与性质2.等边三角形的判定与性质3.含30度角的直角三角形.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源:2015届浙江省八年级下学期期中考试数学试卷(解析版) 题型:解答题
已知关于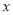 的方程
的方程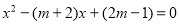
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长.
查看答案和解析>>
科目:初中数学 来源:2015届浙江省嘉兴市八年级下学期期中检测数学试卷(解析版) 题型:选择题
A居民区的月底统计用电情况,其中3户用电45度,5户用电50度,6户用电42度,则平均用电为( )
A.41度 B.42度 C.45.5度 D.46度
查看答案和解析>>
科目:初中数学 来源:2015届河南省郑州市八年级下学期期末考试数学试卷(解析版) 题型:解答题
小华参加学校的社团活动,需要摆放一个平行四边形的木框做道具,他手里有七根木条,长度分别为①40cm②50cm③40cm④60cm⑤50cm⑥90cm⑦100cm,若木条不能折断,请你帮他选一选,用几条可以摆成一个平行四边形?写出一种方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源:2015届河南省郑州市八年级下学期期末考试数学试卷(解析版) 题型:填空题
如图,是一个风筝骨架.为使风筝平衡,须使∠AOP=∠BOP.我们已知PC⊥OA,PD⊥OB,那么PC和PD应满足 _________ ,才能保证OP为∠AOB角平分线.

查看答案和解析>>
科目:初中数学 来源:2015届河北省石家庄市赵县八年级下学期期末考试数学试卷(解析版) 题型:解答题
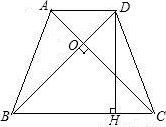
如图,四边形ABCD为等腰梯形,AD∥BC,AB=CD,对角线AC、BD交于点O,且AC⊥BD,DH⊥BC.
(1)求证:DH=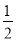 (AD+BC);
(AD+BC);
(2)若AC=6,求梯形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com