
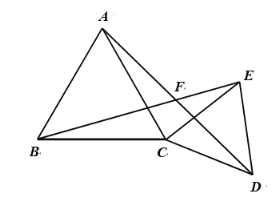
【题目】如图,![]() 和
和![]() 都是等边三角形,连接
都是等边三角形,连接![]() 、
、![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)求证![]() ;
;
(2)![]()
![]() .
.
【答案】(1)证明见解析;(2)60.
【解析】
(1)利用SAS定理证明![]() ≌
≌![]() ,从而求解;(2)利用全等三角形的性质求得
,从而求解;(2)利用全等三角形的性质求得![]() ,然后根据三角形内角和求得∠BFA=180°-(∠BAF+∠ABF),根据等量代换求得∠BFA =180°-(∠BAC+∠ABC),然后利用等边三角形的性质求解.
,然后根据三角形内角和求得∠BFA=180°-(∠BAF+∠ABF),根据等量代换求得∠BFA =180°-(∠BAC+∠ABC),然后利用等边三角形的性质求解.
解:(1)在![]() 和
和![]() 中
中
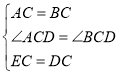
∴![]() ≌
≌![]() (
(![]() )
)
∴![]()
(2)由![]() ≌
≌![]() 得
得![]()
∴∠BFA=180°-(∠BAF+∠ABF)
=180°-(∠BAC+∠CAD+∠ABF)
=180°-(∠BAC+∠CBE+∠ABF)
=180°-(∠BAC+∠ABC)
∵△ABC为等边三角形
∴∠BAC=∠ABC=60°
∴∠BFA=180°-(60°+60°)=60°
故答案为:60


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
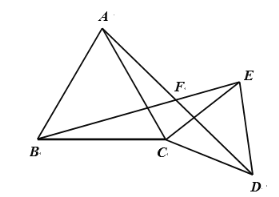
【题目】如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.
(Ⅰ)△ABC的面积等于_____;
(Ⅱ)若四边形DEFG是正方形,且点D,E在边CA上,点F在边AB上,点G在边BC上,请在如图所示的网格中,用无刻度的直尺,画出点E,点G,并简要说明点E,点G的位置是如何找到的(不要求证明)_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若中学生体质健康综合评定成绩为x分,满分为100分.规定:85≤x≤100为A级,75≤x<85为B级,60≤x<75为C级,x<60为D级.现随机抽取某中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图.
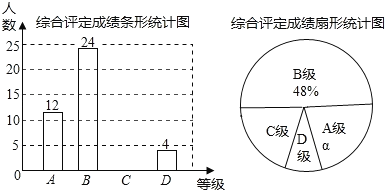
请根据图中的信息,解答下列问题:
(1)在这次调查中,一共抽取了 名学生;
(2)a= %;C级对应的圆心角为 度.
(3)补全条形统计图;
(4)若该校共有2000名学生,请你估计该校D级学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C是半圆O上的一点,CF切半圆O于点C,BD⊥CF于为点D,BD与半圆O交于点E.
(1)求证:BC平分∠ABD.
(2)若DC=8,BE=4,求圆的直径.
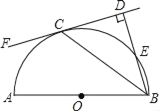
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN是⊙O的直径,点A是半圆上的三等分点,点B是劣弧AN的中点,点P是直径MN上一动点.若MN=2![]() ,AB=1,则△PAB周长的最小值是( )
,AB=1,则△PAB周长的最小值是( )
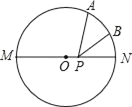
A. 2![]() +1 B.
+1 B. ![]() +1 C. 2 D. 3
+1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快车和慢车分别从A市和B市两地同时出发,匀速行驶,先相向而行,慢车到达A市后停止行驶,快车到达B市后,立即按原路原速度返回A市(调头时间忽略不计),结果与慢车同时到达A市.快、慢两车距B市的路程y1、y2(单位:km)与出发时间x(单位:h)之间的函数图像如图所示.
(1)A市和B市之间的路程是 km;
(2)求a的值,并解释图中点M的横坐标、纵坐标的实际意义;
(3)快车与慢车迎面相遇以后,再经过多长时间两车相距20 km?
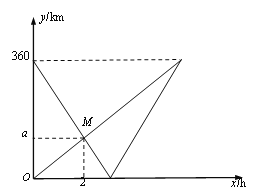
查看答案和解析>>
科目:初中数学 来源: 题型:
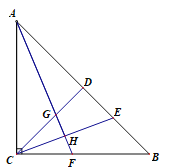
【题目】等腰Rt△ABC,点D为斜边AB上的中点,点E在线段BD上,连结CD,CE,作AH⊥CE,垂足为H,交CD于点G,AH的延长线交BC于点F.
(1)求证:△ADG≌△CDE.
(2)若点H恰好为CE的中点,求证:∠CGF=∠CFG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.
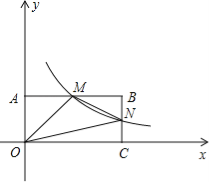
(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com