
分析 (1)由等腰三角形的性质得出∠B=∠C,∠B′=∠C′,由顶角相等和三角形内角和定理得出∠B=∠C=∠B′=∠C′,即可得出△ABC∽△A′B′C′;
(2)由等腰三角形的性质得出∠B=∠C,∠B′=∠C′,再由∠B=∠B′(或∠C=∠C′),得出∠C=∠C′(或∠B=∠B′),即可得出结论.
解答 证明:(1)∵△ABC和△A′B′C′是等腰三角形,∠A、∠A′分别是顶角,
∴∠B=∠C,∠B′=∠C′,
∵∠A=∠A′,∠A+∠B+∠C=180°,∠A′+∠B′+∠C′=180°,
∴∠B=∠C=∠B′=∠C′,
∴△ABC∽△A′B′C′;
(2)∵△ABC和△A′B′C′是等腰三角形,∠A、∠A′分别是顶角,
∴∠B=∠C,∠B′=∠C′,
∵∠B=∠B′,
∴∠C=∠C′,
∴△ABC∽△A′B′C′;
若∠C=∠C′,
同理可证:△ABC∽△A′B′C′.
点评 本题考查了相似三角形的判定方法、等腰三角形的性质、三角形内角和定理;熟练掌握相似三角形的判定方法,弄清等腰三角形的角之间的关系是解决问题的关键.


科目:初中数学 来源: 题型:解答题
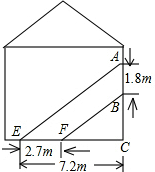 如图,阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区,已知亮区到窗口下的墙脚距离EC=7.2m,窗口高AB=1.8m.求窗口底边离地面的高BC.
如图,阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区,已知亮区到窗口下的墙脚距离EC=7.2m,窗口高AB=1.8m.求窗口底边离地面的高BC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com