
【题目】在平面直角坐标系xOy中,已知点A在抛物线y=x2+bx+c(b>0)上,且A(1,-1),
(1)若b-c=4,求b,c的值;
(2)若该抛物线与y轴交于点B,其对称轴与x轴交于点C,则命题“对于任意的一个k(0<k<1),都存在b,使得OC=k·OB.”是否正确?若正确,请证明;若不正确,请举反例;
(3)将该抛物线平移,平移后的抛物线仍经过(1,-1),点A的对应点A1为
(1-m,2b-1).当m≥-![]() 时,求平移后抛物线的顶点所能达到的最高点的坐标.
时,求平移后抛物线的顶点所能达到的最高点的坐标.
【答案】(1)b=1,c=-3;(2)对于任意的0<k<1,不一定存在b,使得OC=k·OB;(3)平移后抛物线的顶点所能达到的最高点坐标为(![]() ,-
,-![]() ).
).
【解析】
(1)把(1,-1)代入y=x2+bx+c得b+c=-2,与b-c=4构成方程组,解方程组即可求得;
(2)求得B(0,-2-b),C(-![]() ,0),即可求得OC=
,0),即可求得OC=![]() ,OB=2+b,根据题意当k=
,OB=2+b,根据题意当k=![]() 时,由OC=
时,由OC=![]() OB得
OB得![]() =
=![]() (2+b),此时b=-6<0不合题意,即可判定命题不正确;
(2+b),此时b=-6<0不合题意,即可判定命题不正确;
(3)把y=x2+bx+c化成顶点式,得到y=(x+![]() )2-
)2-![]() -2-b,根据平移的规律得到y=(x+
-2-b,根据平移的规律得到y=(x+![]() +m)2-
+m)2-![]() -2+b,把(1,-1)代入,进一步得到(1+
-2+b,把(1,-1)代入,进一步得到(1+![]() +m)2=(
+m)2=(![]() -1)2,即1+
-1)2,即1+![]() +m=±(
+m=±(![]() -1),分类求得m=-b,由m≥-
-1),分类求得m=-b,由m≥-![]() ,得到b≤
,得到b≤![]() ,即0<b≤
,即0<b≤![]() ,从而得到平移后的解析式为y=(x-
,从而得到平移后的解析式为y=(x-![]() )2-
)2-![]() -2+b,得到顶点为(
-2+b,得到顶点为(![]() ,-
,-![]() -2+b),设p=-
-2+b),设p=-![]() -2+b,即p=-
-2+b,即p=-![]() (b-2)2-1,即可得到p取最大值为-
(b-2)2-1,即可得到p取最大值为-![]() ,从而得到最高点的坐标.
,从而得到最高点的坐标.
(1)把(1,-1)代入y=x2+bx+c,可得b+c=-2,
解![]() ,可得b=1,c=-3,
,可得b=1,c=-3,
(2)不正确,
理由:由b+c=-2,得c=-2-b.
对于y=x2+bx+c,
当x=0时,y=c=-2-b.
抛物线的对称轴为直线x=-![]() .
.
所以B(0,-2-b),C(-![]() ,0).
,0).
因为b>0,
所以OC=![]() ,OB=2+b,
,OB=2+b,
当k=![]() 时,由OC=
时,由OC=![]() OB得
OB得![]() =
=![]() (2+b),此时b=-6<0不合题意.
(2+b),此时b=-6<0不合题意.
所以对于任意的0<k<1,不一定存在b,使得OC=kOB;
(3)由平移前的抛物线y=x2+bx+c,可得
y=(x+![]() )2-
)2-![]() +c,即y=(x+
+c,即y=(x+![]() )2-
)2-![]() -2-b.
-2-b.
因为平移后A(1,-1)的对应点为A1(1-m,2b-1)
可知,抛物线向左平移m个单位长度,向上平移2b个单位长度.
则平移后的抛物线解析式为y=(x+![]() +m)2-
+m)2-![]() -2-b+2b,
-2-b+2b,
即y=(x+![]() +m)2-
+m)2-![]() -2+b.
-2+b.
把(1,-1)代入,得
(1+![]() +m)2-
+m)2-![]() -2+b=-1.
-2+b=-1.
(1+![]() +m)2=
+m)2=![]() -b+1.
-b+1.
(1+![]() +m)2=(
+m)2=(![]() -1)2.
-1)2.
所以1+![]() +m=±(
+m=±(![]() -1).
-1).
当1+![]() +m=
+m=![]() -1时,m=-2(不合题意,舍去);
-1时,m=-2(不合题意,舍去);
当1+![]() +m=-(
+m=-(![]() -1)时,m=-b,
-1)时,m=-b,
因为m≥-![]() ,所以b≤
,所以b≤![]() .
.
所以0<b≤![]() ,
,
所以平移后的抛物线解析式为y=(x-![]() )2-
)2-![]() -2+b.
-2+b.
即顶点为(![]() ,-
,-![]() -2+b),
-2+b),
设p=-![]() -2+b,即p=-
-2+b,即p=-![]() (b-2)2-1.
(b-2)2-1.
因为-![]() <0,所以当b<2时,p随b的增大而增大.
<0,所以当b<2时,p随b的增大而增大.
因为0<b≤![]() ,
,
所以当b=![]() 时,p取最大值为-
时,p取最大值为-![]() ,
,
此时,平移后抛物线的顶点所能达到的最高点坐标为(![]() ,-
,-![]() ).
).


科目:初中数学 来源: 题型:
【题目】若某同学在一次综合性测试中,语文、数学、英语、科学、社会5门学科的名次在其所在班级里都不超过3(记第一名为1,第二名为2,第三名为3,以此类推且没有并列名次情况),则称该同学为超级学霸.现根据不同班级的甲、乙、丙、丁四位同学对一次综合性测试名次数据的描述,一定可以推断是超级学霸的是( )
A. 甲同学:平均数为2,中位数为2B. 乙同学:中位数是2,唯一的众数为2
C. 丙同学:平均数是2,标准差为2D. 丁同学:平均数为2,唯一的众数为2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,∠B=∠C,D,E分别是线段BC,AC上的一点,且AD=AE,
(1)如图1,若∠BAC=90°,D是BC中点,则∠2的度数为_____;
(2)借助图2探究并直接写出∠1和∠2的数量关系_____.
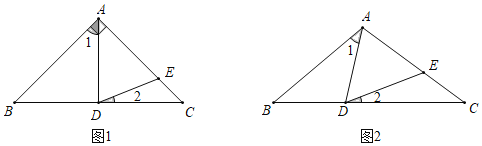
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,DE是△ADC的高,DF是△ABD的中线,且CE=1,DE=2,AE=4.
(1)∠ADC是直角吗?请说明理由.
(2)求DF的长.
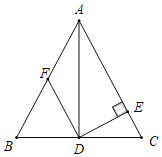
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(4,2).将点A绕坐标原点O旋转90°后,再向左平移1个单位长度得到点A′,则过点A′的正比例函数的解析式为_____.
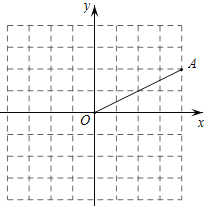
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学学习中,及时对知识进行归纳和整理是改善学习的重要方法.善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,对照图形,把相关知识归纳整理如下:
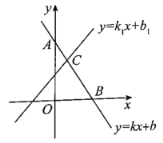
一次函数与方程(组)的关系:

一次函数与不等式的关系:

(1)请你根据以上方框中的内容在下面的数字序号后写出相应的结论:
①______________________; ②______________________,
③______________________; ④______________________.
(2)如果点C的坐标为![]() ,那么不等式
,那么不等式![]() 的解集是___________.
的解集是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“绿水青山就是金山银山”的发展理念,某市政部门招标一工程队负责在山脚下修建一座水库的土方施工任务.该工程队有![]() 两种型号的挖掘机,已知3台
两种型号的挖掘机,已知3台![]() 型和5台
型和5台![]() 型挖掘机同时施工一小时挖土165立方米;4台
型挖掘机同时施工一小时挖土165立方米;4台![]() 型和7台
型和7台![]() 型挖掘机同时施工一小时挖土225立方米.每台
型挖掘机同时施工一小时挖土225立方米.每台![]() 型挖掘机一小时的施工费用为300元,每台
型挖掘机一小时的施工费用为300元,每台![]() 型挖掘机一小时的施工费用为180元.
型挖掘机一小时的施工费用为180元.
(1)分别求每台![]() 型,
型, ![]() 型挖掘机一小时挖土多少立方米?
型挖掘机一小时挖土多少立方米?
(2)若不同数量的![]() 型和
型和![]() 型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发商以每件50元的价格购进400件T恤.若以单价70元销售,预计可售出200件.批发商的销售策略是:第一个月为增加销售量,降价销售,经过市场调查,单价每降低0.5元,可多售出5件,但最低单价不低于购进的价格;第一个月结束后,将剩余的T恤一次性清仓销售,清仓时单价为40元.设第一个月单价降低x元.
(1)根据题意,完成下表:
每件T恤的利润(元) | 销售量(件) | |
第一个月 | ||
清仓时 |
(2)T恤的销售单价定为多少元时,该批发商可获得最大利润?最大利润为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com