
【题目】为落实“绿水青山就是金山银山”的发展理念,某市政部门招标一工程队负责在山脚下修建一座水库的土方施工任务.该工程队有![]() 两种型号的挖掘机,已知3台
两种型号的挖掘机,已知3台![]() 型和5台
型和5台![]() 型挖掘机同时施工一小时挖土165立方米;4台
型挖掘机同时施工一小时挖土165立方米;4台![]() 型和7台
型和7台![]() 型挖掘机同时施工一小时挖土225立方米.每台
型挖掘机同时施工一小时挖土225立方米.每台![]() 型挖掘机一小时的施工费用为300元,每台
型挖掘机一小时的施工费用为300元,每台![]() 型挖掘机一小时的施工费用为180元.
型挖掘机一小时的施工费用为180元.
(1)分别求每台![]() 型,
型, ![]() 型挖掘机一小时挖土多少立方米?
型挖掘机一小时挖土多少立方米?
(2)若不同数量的![]() 型和
型和![]() 型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
【答案】(1)每台![]() 型挖掘机一小时挖土30立方米,每台
型挖掘机一小时挖土30立方米,每台![]() 型挖据机一小时挖土15立方米;
型挖据机一小时挖土15立方米;
(2)共有三种调配方案.方案一: ![]() 型挖据机7台,
型挖据机7台,![]() 型挖掘机5台;方案二:
型挖掘机5台;方案二: ![]() 型挖掘机8台,
型挖掘机8台,![]() 型挖掘机4台;方案三:
型挖掘机4台;方案三: ![]() 型挖掘机9台,
型挖掘机9台,![]() 型挖掘机3台.当A型挖掘机7台,
型挖掘机3台.当A型挖掘机7台, ![]() 型挖掘机5台的施工费用最低,最低费用为12000元.
型挖掘机5台的施工费用最低,最低费用为12000元.
【解析】(1)根据题意列出方程组即可;
(2)利用总费用不超过12960元求出方案数量,再利用一次函数增减性求出最低费用.
(1)设每台![]() 型,
型,![]() 型挖掘机一小时分别挖土
型挖掘机一小时分别挖土![]() 立方米和
立方米和![]() 立方米,根据题意,得
立方米,根据题意,得
![]()
解得![]()
所以,每台![]() 型挖掘机一小时挖土30立方米,每台
型挖掘机一小时挖土30立方米,每台![]() 型挖据机一小时挖土15立方米.
型挖据机一小时挖土15立方米.
(2)设![]() 型挖掘机有
型挖掘机有![]() 台,总费用为
台,总费用为![]() 元,则
元,则![]() 型挖据机有
型挖据机有![]() 台.根据题意,得
台.根据题意,得
![]()
![]() ,
,
因为![]() ,解得
,解得![]() ,
,
又因为![]() ,解得
,解得![]() ,所以
,所以![]() .
.
所以,共有三种调配方案.
方案一:当![]() 时,
时,![]() ,即
,即![]() 型挖据机7台,
型挖据机7台,![]() 型挖掘机5台;
型挖掘机5台;
方案二:当![]() 时,
时,![]() ,即
,即![]() 型挖掘机8台,
型挖掘机8台,![]() 型挖掘机4台;
型挖掘机4台;
方案三:当![]() 时,
时,![]() ,即
,即![]() 型挖掘机9台,
型挖掘机9台,![]() 型挖掘机3台.
型挖掘机3台.
![]() ,由一次函数的性质可知,
,由一次函数的性质可知,![]() 随
随![]() 的减小而减小,
的减小而减小,
当![]() 时,
时,![]() ,
,
此时![]() 型挖掘机7台,
型挖掘机7台, ![]() 型挖掘机5台的施工费用最低,最低费用为12000元.
型挖掘机5台的施工费用最低,最低费用为12000元.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:
【题目】某儿童游乐场为了有稳定的客源,决定开办会员业务,每张会员证30元,只限本人使用,有效期为一年,凭证入场每人次收费2元,不凭证入场每人次收费3元.
(1)一年内在这个游乐场玩多少次,办理会员证和不办理会员证花钱一样多?
(2)2019年,小明计划每月到游乐场玩4次,请你为他推荐一种经济省钱的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,已知点A(m,0),B(n,0),且m,n满足(m+1)2+![]() =0,将线段AB向右平移1个单位长度,再向上平移2个单位长度,得到线段CD,其中点C与点A对应,点D与点B对应,连接AC,BD.
=0,将线段AB向右平移1个单位长度,再向上平移2个单位长度,得到线段CD,其中点C与点A对应,点D与点B对应,连接AC,BD.
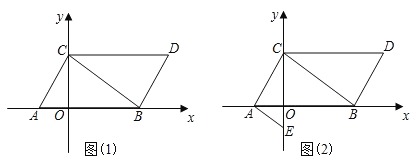
(1)求点A、B、C、D的坐标;
(2)在x轴上是否存在点P,使三角形PBC的面积等于平行四边形ABDC的面积?若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(2),点E在y轴的负半轴上,且∠BAE=∠DCB.求证:AE∥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,﹣300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是( )
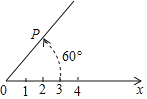
A. Q(3,240°) B. Q(3,﹣120°) C. Q(3,600°) D. Q(3,﹣500°)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C在一次函数![]() 的图象上,它们的横坐标依次为
的图象上,它们的横坐标依次为![]() ,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )
,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )

A. 1 B. 3 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图直线![]() 的解析式为y=x+1,直线
的解析式为y=x+1,直线![]() 的解析式为
的解析式为![]() ;这两个图象交于y轴上一点C,直线
;这两个图象交于y轴上一点C,直线![]() 与x轴的交点B(2,0).
与x轴的交点B(2,0).
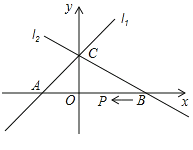
(1)求a、b的值;
(2)动点P从点B出发沿x轴以每秒1个单位长的速度向左移动,设移动时间为t秒,当△PAC为等腰三角形时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知A(-1,4),B(4,2),C(-1,0)三点.
(1)点A关于y轴的对称点A′ 的坐标为 ,点B关于x轴的对称点B′ 的坐标为 ,线段AC的垂直平分线与y轴的交点D的坐标为 ;
(2)求(1)中的△A′ B′ D的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:已知,如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD
求证:∠EGF=90°
证明:∵HG∥AB(已知)
∴∠1=∠3(__________________________)
又∵HG∥CD(已知)
∴∠2=∠4(_______________________________)
∵AB∥CD(已知)
∴∠BEF+___________=180°(_____________________)
又∵EG平分∠BEF,FG平分∠EFD (已知)
∴∠1=(______)∠BEF,∠2=(______)∠EFD (______________________)
∴∠1+∠2=(________) (∠BEF +∠EFD)=(____________)
∴∠3+∠4=90°(_______________________)即∠EGF=90°

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解学生课外阅读的情况,对学生“平均每天课外阅读的时间”进行了随机抽样调查,如图是根据调查结果绘制的两幅不完整的统计图.请你根据统计图提供的信息,解答以下问题: 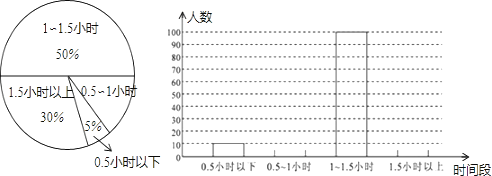
(1)平均每天课外阅读的时间为“0.5~1小时”部分的扇形图的圆心角为多少度;
(2)本次一共调查了多少名学生;
(3)将条形图补充完整;
(4)若该校有1680名学生,请估计该校有多少名学生平均每天课外阅读的时间在0.5小时以下.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com