
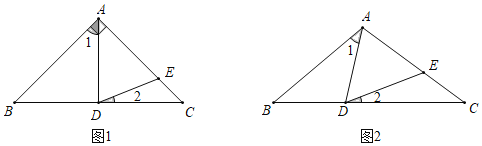
【题目】已知:在△ABC中,∠B=∠C,D,E分别是线段BC,AC上的一点,且AD=AE,
(1)如图1,若∠BAC=90°,D是BC中点,则∠2的度数为_____;
(2)借助图2探究并直接写出∠1和∠2的数量关系_____.
【答案】22.5 ∠1=2∠2
【解析】
(1)根据三角形的一个外角等于和它不相邻的两个内角的和,∠AED=∠EDC+∠C,∠ADC=∠B+∠BAD,再根据等边对等角的性质∠B=∠C,∠ADE=∠AED,进而得出∠BAD=2∠CDE.
(2)根据三角形的一个外角等于和它不相邻的两个内角的和,∠AED=∠EDC+∠C,∠ADC=∠B+∠BAD,再根据等边对等角的性质∠B=∠C,∠ADE=∠AED,进而得出∠BAD=2∠CDE.
解:(1)∠AED=∠CDE+∠C,∠ADC=∠B+∠BAD,
∵AD=AE,
∴∠AED=∠ADE,
∵∠B=∠C,∠BAC=90°,D是BC中点,
∴∠BAD=45°,
∴∠B+∠BAD=∠EDC+∠C+∠CDE,
即∠BAD=2∠CDE,
∴∠2=22.5°;
(2)∠AED=∠CDE+∠C,∠ADC=∠B+∠BAD,
∵AD=AE,
∴∠AED=∠ADE,
∵AB=AC,
∴∠B=∠C,
∴∠B+∠BAD=∠EDC+∠C+∠CDE,
即∠BAD=2∠CDE,∠1=2∠2.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
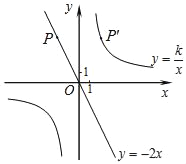
【题目】如图,已知直线y=﹣2x经过点P(﹣2,a),点P关于y轴的对称点P′在反比例函数y=![]() (k≠0)的图象上.
(k≠0)的图象上.
(1)求反比例函数的解析式;
(2)直接写出当y<4时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 的对称轴是
的对称轴是![]() 且经过
且经过![]() 、
、![]() 两点,与
两点,与![]() 轴的另一交点为点
轴的另一交点为点![]() ,连结
,连结![]() .
.
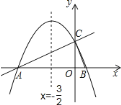
(1)填空:点![]() 、点
、点![]() 和点
和点![]() 的坐标分别为
的坐标分别为![]() ________,
________,![]() ________,
________,![]() ________;
________;
(2)求证:![]() ;
;
(3)求抛物线解析式;
(4)若点![]() 为直线
为直线![]() 上方的抛物线上的一点,连结
上方的抛物线上的一点,连结![]() ,
,![]() ,求
,求![]() 面积的最大值,并求出此时点
面积的最大值,并求出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )

A.平均数是6
B.中位数是6.5
C.众数是7
D.平均每周锻炼超过6小时的人数占该班人数的一半
查看答案和解析>>
科目:初中数学 来源: 题型:
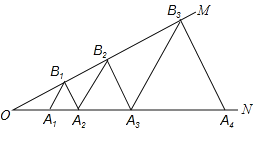
【题目】如图,∠MON=30°,点A1、A2、A3、……在射线ON上,点B1、B2、B3、……在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4,……均为等边三角形,若OA1=1,则△A2019B2019A2020的边长为__________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形方格纸中,我们把顶点都在“格点”上的三角形称为“格点三角形“,如图,△ABC是一个格点三角形,点A的坐标为(﹣1,2).
(1)点B的坐标为 ,△ABC的面积为 ;
(2)在所给的方格纸中,请你以原点O为位似中心,将△ABC放大为原来的2倍,放大后点A、B的对应点分别为A1、B1,点B1在第一象限;
(3)在(2)中,若P(a,b)为线段AC上的任一点,则放大后点P的对应点P1的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的反称点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=2r,则称P′为点P关于⊙C的反称点,如图为点P及其关于⊙C的反称点P′的示意图.
特别地,当点P′与圆心C重合时,规定CP′=0.
(1)当⊙O的半径为1时.
①分别判断点M(2,1),N(![]() ,0),T(1,
,0),T(1, ![]() )关于⊙O的反称点是否存在?若存在,求其坐标;
)关于⊙O的反称点是否存在?若存在,求其坐标;
②点P在直线y=﹣x+2上,若点P关于⊙O的反称点P′存在,且点P′不在x轴上,求点P的横坐标的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线y=﹣![]() x+2
x+2![]() 与x轴、y轴分别交于点A,B,若线段AB上存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.
与x轴、y轴分别交于点A,B,若线段AB上存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A在抛物线y=x2+bx+c(b>0)上,且A(1,-1),
(1)若b-c=4,求b,c的值;
(2)若该抛物线与y轴交于点B,其对称轴与x轴交于点C,则命题“对于任意的一个k(0<k<1),都存在b,使得OC=k·OB.”是否正确?若正确,请证明;若不正确,请举反例;
(3)将该抛物线平移,平移后的抛物线仍经过(1,-1),点A的对应点A1为
(1-m,2b-1).当m≥-![]() 时,求平移后抛物线的顶点所能达到的最高点的坐标.
时,求平移后抛物线的顶点所能达到的最高点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂按用户的月需求量![]() (件)完成一种产品的生产,其中
(件)完成一种产品的生产,其中![]() .每件的售价为18万元,每件的成本
.每件的售价为18万元,每件的成本![]() (万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量
(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量![]() (件)成反比.经市场调研发现,月需求量
(件)成反比.经市场调研发现,月需求量![]() 与月份
与月份![]() (
(![]() 为整数,
为整数,![]() )符合关系式
)符合关系式![]() (
(![]() 为常数),且得到了表中的数据.
为常数),且得到了表中的数据.
月份 | 1 | 2 |
成本 | 11 | 12 |
需求量 | 120 | 100 |
(1)求![]() 与
与![]() 满足的关系式,请说明一件产品的利润能否是12万元;
满足的关系式,请说明一件产品的利润能否是12万元;
(2)求![]() ,并推断是否存在某个月既无盈利也不亏损;
,并推断是否存在某个月既无盈利也不亏损;
(3)在这一年12个月中,若第![]() 个月和第
个月和第![]() 个月的利润相差最大,求
个月的利润相差最大,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com