
����Ŀ����ƽ��ֱ������ϵxOy�У���C�İ뾶Ϊr��P����Բ��C���غϵĵ㣬��P������C�ķ��Ƶ�Ķ������£���������CP�ϴ���һ��P�䣬����CP+CP��=2r�����P��Ϊ��P������C�ķ��Ƶ㣬��ͼΪ��P���������C�ķ��Ƶ�P���ʾ��ͼ��
�ر�أ�����P����Բ��C�غ�ʱ���涨CP��=0��
��1������O�İ뾶Ϊ1ʱ��
���ֱ��жϵ�M��2��1����N��![]() ��0����T��1��
��0����T��1�� ![]() ��������O�ķ��Ƶ��Ƿ���ڣ������ڣ��������ꣻ
��������O�ķ��Ƶ��Ƿ���ڣ������ڣ��������ꣻ
����P��ֱ��y=��x+2�ϣ�����P������O�ķ��Ƶ�P����ڣ��ҵ�P�䲻��x���ϣ����P�ĺ������ȡֵ��Χ��
��2����C��Բ����x���ϣ��뾶Ϊ1��ֱ��y=��![]() x+2
x+2![]() ��x�ᡢy��ֱ��ڵ�A��B�����߶�AB�ϴ��ڵ�P��ʹ�õ�P������C�ķ��Ƶ�P������C���ڲ�����Բ��C�ĺ������ȡֵ��Χ��
��x�ᡢy��ֱ��ڵ�A��B�����߶�AB�ϴ��ڵ�P��ʹ�õ�P������C�ķ��Ƶ�P������C���ڲ�����Բ��C�ĺ������ȡֵ��Χ��

���𰸡���1��������������0��x��2����2��Բ��C�ĺ������ȡֵ��Χ��2��x��8��
�������������������1�� �����ݷ��Ƶ�Ķ��廭ͼ�ó����ۣ��ڡ�CP��2r��2 CP2��4�� P��x����x��2���� CP2��x2������x��2��2��2x2��4x��4����2x2��4x��0�� x��x��2����0����0��x��2����x��2��x=0������֤���ɵó���P��2��0����P����2��0������������P��0��2����P����0��0�����������⣬��0��x��2
��2�����A��B�����꣬�ó�OA��OB�ı�ֵ���Ӷ������OAB=30������C��x��0��
����C��OA��ʱ����CH��AB��H����CH��CP��2r��2����AC��4���ó� C�������x��2�� ����x��2ʱ��C�����꣨2��0����H��ķ��Ƶ�H����2��0����Բ���ڲ���������C��A���Ҳ�ʱ��C���߶�AB�ľ���ΪAC����AC���ֵΪ2����C�������x��8���ó�����.
��������� ��1���⣺��M��2��1�������ڣ� ![]() ���ڣ����Ƶ�
���ڣ����Ƶ�![]()
![]() ���ڣ����Ƶ�T����0��0��
���ڣ����Ƶ�T����0��0��
�ڡ�CP��2r��2 CP2��4�� P��x����x��2���� CP2��x2������x��2��2��2x2��4x��4��4
2x2��4x��0�� x��x��2����0����0��x��2����x��2ʱ��P��2��0����P����2��0������������
��x��0ʱ��P��0��2����P����0��0�����������⣬��0��x��2
��2���⣺������ã�A��6��0����![]() ����
����![]() �����OAB��30������C��x��0��
�����OAB��30������C��x��0��
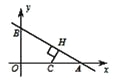
����C��OA��ʱ����CH��AB��H����CH��CP��2r��2����AC��4�� C�������x��2��
����x��2ʱ��C�����꣨2��0����H��ķ��Ƶ�H����2��0����Բ���ڲ���
����C��A���Ҳ�ʱ��C���߶�AB�ľ���ΪAC����AC���ֵΪ2����C�������x��8
����������Բ��C�ĺ������ȡֵ��Χ2��x��8��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x��y�Ķ�Ԫһ�η�����![]() �ĽⶼΪ������
�ĽⶼΪ������
��1����a��ȡֵ��Χ��
��2������|a+1|��|a��1|��
��3����������Ԫһ�η�����Ľ���һ�����������ε�һ������һ���ױߵij�����������������ε��ܳ�Ϊ9����a��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУҪ��չУ�����ڻ��Ϊ�˺������Ž�Ŀ����ѧ����ϲ���ĸ������赸��СƷ�����������Ŀ������һ������������飨ÿ��ѧ������ѡ����ֻ��ѡ��һ�ࣩ���������������Ƴ�����������������ͳ��ͼ.
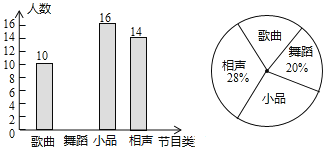
�����ͼ����Ϣ���ش��������⣺
��1�����ι�������_________��ѧ��.
��2��������ͳ��ͼ�У����������������ε�Բ�Ľǵ���_________��.
��3����ȫ����ͳ��ͼ������עƵ����.
��4����������ͳ�Ʒ��������Ƹ�У2000��ѧ������ϲ��СƷ������Լ�ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2��bx��c(a��0)�IJ���ͼ���䶥������Ϊ(1��n)����������x���һ�������ڵ�(3��0)��(4��0)֮�䣮�����н���

��a��b��c��0����3a��b��0��
��b2��4a(c��n)��
��һԪ���η���ax2��bx��c��n��1����������ȵ�ʵ������
������ȷ���۵ĸ�����(����)
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����10��10�������������У�ÿ��С�����εı߳���Ϊ1����������һ������ABC���������εĶ��㶼�ڸ���ϣ���
��1����ͼ��������ABC����ֱ��l�ԳƵġ�A1B1C1����Ҫ��A��A1��B��B1��C��C1���Ӧ��
��2���ڣ�1���ʵĽ���£�����BB1��CC1�����ı���BB1C1C�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
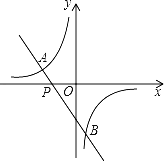
����Ŀ����֪����ͼ��һ�κ���y=��2x��3��ͼ���뷴��������y=![]() ��m��0����ͼ���ཻ�ڵ�A����2��1���͵�B��
��m��0����ͼ���ཻ�ڵ�A����2��1���͵�B��
��1�����������Ľ���ʽ��
��2�����B�����ꣻ
��3������ͼ��ش𣺵�x��ʲô��Χ��ȡֵʱ��һ�κ����ĺ���ֵС�ڷ����������ĺ���ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���A��60����AD��8��F��AB���е㣮����F��FE��AD������ΪE.����AEF�ص�A����B�ķ���ƽ�ƣ��õ���A��E��F��.��P��P���ֱ���EF��E��F�����е㣬����A�����B�غ�ʱ���ı���PP��F��F�����Ϊ( ����)

A. 8![]() B. 4
B. 4![]() C. 12
C. 12![]() D. 8
D. 8![]() ��8
��8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С����P��������ر�ƫ��60�㷽����ʻ����A�������������Ϸ�����ʻ100��![]() +1������B������B���۲����ʱ���ڵ�P���ڱ�ƫ��45�㷽���ϣ�P��A�����������ף�
+1������B������B���۲����ʱ���ڵ�P���ڱ�ƫ��45�㷽���ϣ�P��A�����������ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������AEFG�Ķ���E��G�ֱ���������ABCD��AB��AD���ϣ�����B����EF�ڵ�M����FG�ڵ�N����AE=a��AG=b��AB=c��b��a��c����
��1����֤�� ![]() ��
��
��2������AMN���������a��b��c�Ĵ���ʽ��ʾ����
��3������MAN=45��ʱ����֤��c2=2ab��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com