
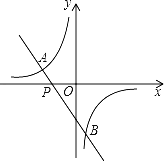
【题目】已知:如图,一次函数y=﹣2x﹣3的图象与反比例函数y=![]() (m≠0)的图象相交于点A(﹣2,1)和点B.
(m≠0)的图象相交于点A(﹣2,1)和点B.
(1)求反比例函数的解析式;
(2)求点B的坐标;
(3)根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?
科目:初中数学 来源: 题型:
【题目】试解答下列问题:
(1)在图1我们称之为“8字形”,请直接写出∠A、∠B、∠C、∠D之间的数量关系: ;
(2)仔细观察,在图2中“8字形”的个数是 个;
(3) 在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试求∠P的度数;
(4)如果图2中∠D和∠B为任意角时,其他条件不变,试写出∠B与∠P、∠D之间数量关系 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F. 若AB=6,BC=![]() ,则FD的长为( )
,则FD的长为( )
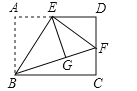
A. 2B. 4C. 6D. 23
查看答案和解析>>
科目:初中数学 来源: 题型:
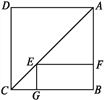
【题目】如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为E,F,若正方形ABCD的周长是40 cm.
(1)求证:四边形BFEG是矩形;
(2)求四边形EFBG的周长;
(3)当AF的长为多少时,四边形BFEG是正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的反称点的定义如下:若在射线CP上存在一点P′,满足CP+CP′=2r,则称P′为点P关于⊙C的反称点,如图为点P及其关于⊙C的反称点P′的示意图.
特别地,当点P′与圆心C重合时,规定CP′=0.
(1)当⊙O的半径为1时.
①分别判断点M(2,1),N(![]() ,0),T(1,
,0),T(1, ![]() )关于⊙O的反称点是否存在?若存在,求其坐标;
)关于⊙O的反称点是否存在?若存在,求其坐标;
②点P在直线y=﹣x+2上,若点P关于⊙O的反称点P′存在,且点P′不在x轴上,求点P的横坐标的取值范围;
(2)⊙C的圆心在x轴上,半径为1,直线y=﹣![]() x+2
x+2![]() 与x轴、y轴分别交于点A,B,若线段AB上存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.
与x轴、y轴分别交于点A,B,若线段AB上存在点P,使得点P关于⊙C的反称点P′在⊙C的内部,求圆心C的横坐标的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小强作出边长为1的第1个等边△A1B1C1,计算器面积为S1,然后分别取△A1B1C1三边的中点A2、B2、C1,作出第2个等边△A2B2C2,计算其面积为S2,用同样的方法,作出第3个等边△A3B3C3,计算其面积为S3,按此规律进行下去,…,由此可得,第20个等边△A20B20C20的面积S20=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是计算机中的一种益智小游戏“扫雷”的画面,在一个![]() 的小方格的正方形 雷区中,随机埋藏着
的小方格的正方形 雷区中,随机埋藏着![]() 颗地雷,每个小方格内最多只能埋藏
颗地雷,每个小方格内最多只能埋藏![]() 颗地雷。小红在游戏开始时首先随机的点击一个方格,该方格中出现了数字“
颗地雷。小红在游戏开始时首先随机的点击一个方格,该方格中出现了数字“![]() ”,其意义表示该格的外围区域(图中阴影部分,记为
”,其意义表示该格的外围区域(图中阴影部分,记为![]() 区域)有
区域)有![]() 颗地雷;接着小红又点击了左上角第一个方格,出现了数字“
颗地雷;接着小红又点击了左上角第一个方格,出现了数字“![]() ”,其外围区域(图中阴影)记为
”,其外围区域(图中阴影)记为![]() 区域;
区域;![]() 区域与
区域与![]() 区域以及出现数字“
区域以及出现数字“![]() ”和“
”和“![]() ”两格以外的部分记为
”两格以外的部分记为![]() 区域。请分别计算出
区域。请分别计算出![]() 区、
区、![]() 区、
区、![]() 区点中地雷的概率,那么她应点击
区点中地雷的概率,那么她应点击![]() 、
、![]() 、
、![]() 中的哪个区域?
中的哪个区域?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B,C,D均在⊙O上,CD为∠ACE的角平分线.
(1)求证:△ABD为等腰三角形;
(2)若∠DCE=45°,BD=6,求⊙O的半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com