
【题目】矩形AOCD绕顶点A(0,5)逆时针方向旋转,当旋转到如图所示的位置时,边BE交边CD于M,且ME=2,CM=4.
(1)求AD的长;
(2)求阴影部分的面积和直线AM的解析式;
(3)求经过A、B、D三点的抛物线的解析式;
(4)在抛物线上是否存在点P,使S△PAM=![]() ?若存在,求出P点坐标;若不存在,请说明理由.
?若存在,求出P点坐标;若不存在,请说明理由.
【答案】
(1)
解:作BP⊥AD于P,BQ⊥MC于Q,如图1,

∵矩形AOCD绕顶点A(0,5)逆时针方向旋转得到矩形ABEF,
∴AB=AO=5,BE=OC=AD,∠ABE=90°,
∵∠PBQ=90°,
∴∠ABP=∠MBQ,
∴Rt△ABP∽Rt△MBQ,
∴![]() ,
,
设BQ=PD=x,AP=y,则AD=x+y,BM=x+y﹣2,
∴![]() ,
,
∴PBMQ=xy,
∵PB﹣MQ=DQ﹣MQ=DM=1,
∴(PB﹣MQ)2=1,即PB2﹣2PBMQ+MQ2=1,
∴52﹣y2﹣2xy+(x+y﹣2)2﹣x2=1,解得x+y=7,
∴BM=5,
∴BE=BM+ME=5+2=7,
∴AD=7;
(2)
解:∵AB=BM,
∴Rt△ABP≌Rt△MBQ,
∴BQ=PD=7﹣AP,MQ=AP,
∵BQ2+MQ2=BM2,
∴(7﹣MQ)2+MQ2=52,解得MQ=4(舍去)或MQ=3,
∴BQ=7﹣3=4,
∴S阴影部分=S梯形ABQD﹣S△BQM
=![]() ×(4+7)×4﹣
×(4+7)×4﹣![]() ×4×3
×4×3
=16;
设直线AM的解析式为y=kx+b,
把A(0,5),M(7,4)代入得![]() ,解得
,解得 ,
,
∴直线AM的解析式为y=﹣![]() x+5;
x+5;
(3)
解:设经过A、B、D三点的抛物线的解析式为y=ax2+bx+c,
∵AP=MQ=3,BP=DQ=4,
∴B(3,1),
而A(0,5),D(7,5),
∴ ,解得
,解得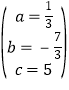 ,
,
∴经过A、B、D三点的抛物线的解析式为y=![]() x2﹣
x2﹣![]() x+5;
x+5;
(4)
解:当点P在线段AM的下方的抛物线上时,作PK∥y轴交AM于K,如图2

设P(x,![]() ﹣
﹣![]() x+5),则K(x,﹣
x+5),则K(x,﹣![]() x+5),则KP=﹣
x+5),则KP=﹣![]() +
+![]() x,根据三角形面积公式可得到
x,根据三角形面积公式可得到![]() (﹣
(﹣![]() x2+
x2+![]() x)7=
x)7=![]() ,解得x1=3,x2=
,解得x1=3,x2=![]() ,于是得到此时P点坐标为(3,1)、(
,于是得到此时P点坐标为(3,1)、(![]() ,
,![]() );再求出过点(3,1)与(
);再求出过点(3,1)与(![]() ,
,![]() )的直线l的解析式为y=﹣
)的直线l的解析式为y=﹣![]() x+
x+![]() ,则可得到直线l与y轴的交点A′的坐标为(0,
,则可得到直线l与y轴的交点A′的坐标为(0,![]() ),所以AA′=
),所以AA′=![]() ,然后把直线AM向上平移
,然后把直线AM向上平移![]() 个单位得到l′,直线l′与抛物线的交点即为P点,由于A″(0,
个单位得到l′,直线l′与抛物线的交点即为P点,由于A″(0,![]() ),则直线l′的解析式为y=﹣
),则直线l′的解析式为y=﹣![]() x+
x+![]() ,再通过解方程组
,再通过解方程组 得P点坐标为(3,1)、
得P点坐标为(3,1)、
(![]() )、(
)、(![]() )、(
)、(![]() ).
).
【解析】
(1)作BP⊥AD于P,BQ⊥MC于Q,如图1,根据旋转的性质得AB=AO=5,BE=OC=AD,∠ABE=90°,利用等角的余角相等得∠ABP=∠MBQ,可证明Rt△ABP∽Rt△MBQ得到![]() ,设BQ=PD=x,AP=y,则AD=x+y,所以BM=x+y﹣2,利用比例性质得到PBMQ=xy,而PB﹣MQ=DQ﹣MQ=DM=1,利用完全平方公式和勾股定理得到52﹣y2﹣2xy+(x+y﹣2)2﹣x2=1,解得x+y=7,则BM=5,BE=BM+ME=7,所以AD=7;
,设BQ=PD=x,AP=y,则AD=x+y,所以BM=x+y﹣2,利用比例性质得到PBMQ=xy,而PB﹣MQ=DQ﹣MQ=DM=1,利用完全平方公式和勾股定理得到52﹣y2﹣2xy+(x+y﹣2)2﹣x2=1,解得x+y=7,则BM=5,BE=BM+ME=7,所以AD=7;
(2)由AB=BM可判断Rt△ABP≌Rt△MBQ,则BQ=PD=7﹣AP,MQ=AP,利用勾股定理得到(7﹣MQ)2+MQ2=52,解得MQ=4(舍去)或MQ=3,则BQ=4,根据三角形面积公式和梯形面积公式,利用S阴影部分=S梯形ABQD﹣S△BQM进行计算即可;然后利用待定系数法求直线AM的解析式;
(3)先确定B(3,1),然后利用待定系数法求抛物线的解析式;
(4)当点P在线段AM的下方的抛物线上时,作PK∥y轴交AM于K,如图2设P(x,![]() ﹣
﹣![]() x+5),则K(x,﹣
x+5),则K(x,﹣![]() x+5),则KP=﹣
x+5),则KP=﹣![]() +
+![]() x,根据三角形面积公式得到
x,根据三角形面积公式得到![]() (﹣
(﹣![]() x2+
x2+![]() x)7=
x)7=![]() ,解得x1=3,x2=
,解得x1=3,x2=![]() ,于是得到此时P点坐标为(3,1)、(
,于是得到此时P点坐标为(3,1)、(![]() ,
,![]() );再求出过点(3,1)与(
);再求出过点(3,1)与(![]() ,
,![]() )的直线l的解析式为y=﹣
)的直线l的解析式为y=﹣![]() x+
x+![]() ,则可得到直线l与y轴的交点A′的坐标为(0,
,则可得到直线l与y轴的交点A′的坐标为(0,![]() ),所以AA′=
),所以AA′=![]() ,然后把直线AM向上平移
,然后把直线AM向上平移![]() 个单位得到l′,直线l′与抛物线的交点即为P点,由于A″(0,
个单位得到l′,直线l′与抛物线的交点即为P点,由于A″(0,![]() ),则直线l′的解析式为y=﹣
),则直线l′的解析式为y=﹣![]() x+
x+![]() ,再通过解方程组
,再通过解方程组 得P点坐标.
得P点坐标.
【考点精析】本题主要考查了二次函数图象的平移的相关知识点,需要掌握平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC、BC及AB的延长线交于点D、E、F,且BF=BC,⊙O是△BEF的外接圆,连接BD. 
(1)求证:BD是⊙O的切线;
(2)求证:DEAC=BECE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=ax2+bx+![]() (a≠0)经过点A(﹣1,0)和B(3,0).
(a≠0)经过点A(﹣1,0)和B(3,0).
(1)求抛物线C1的解析式,并写出其顶点C的坐标;
(2)如图1,把抛物线C1沿着直线AC方向平移到某处时得到抛物线C2 , 此时点A,C分别平移到点D,E处.设点F在抛物线C1上且在x轴的下方,若△DEF是以EF为底的等腰直角三角形,求点F的坐标;
(3)如图2,在(2)的条件下,设点M是线段BC上一动点,EN⊥EM交直线BF于点N,点P为线段MN的中点,当点M从点B向点C运动时:①tan∠ENM的值如何变化?请说明理由;②点M到达点C时,直接写出点P经过的路线长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大学毕业生小王响应国家“自主创业”的号召,利用银行小额无息贷款开办了一家饰品店.该店购进一种今年新上市的饰品进行销售,饰品的进价为每件40元,售价为每件60元,每月可卖出300件.市场调查反映:调整价格时,售价每涨1元每月要少卖10件;售价每下降1元每月要多卖20件.为了获得更大的利润,现将饰品售价调整为60+x(元/件)(x>0即售价上涨,x<0即售价下降),每月饰品销量为y(件),月利润为w(元).
(1)
直接写出y与x之间的函数关系式;
(2)如何确定销售价格才能使月利润最大?求最大月利润;
(3)为了使每月利润不少于6000元应如何控制销售价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】质地均匀的小正方体,六个面分别有数字“1”、“2”、“3”、“4”、“5”、“6”,同时投掷两枚,观察朝上一面的数字.
(1)求数字“1”出现的概率;
(2)求两个数字之和为偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c与x轴交于点A、B,与直线AC:y=﹣x﹣6交y轴于点C,点D是抛物线的顶点,且横坐标为﹣2.
(1)求出抛物线的解析式.
(2)判断△ACD的形状,并说明理由.
(3)直线AD交y轴于点F,在线段AD上是否存在一点P,使∠ADC=∠PCF?若存在,直接写出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+2与坐标轴交于A、B、C三点,其中B(4,0)、C(﹣2,0),连接AB、AC,在第一象限内的抛物线上有一动点D,过D作DE⊥x轴,垂足为E,交AB于点F.
(1)求此抛物线的解析式;
(2)在DE上作点G,使G点与D点关于F点对称,以G为圆心,GD为半径作圆,当⊙G与其中一条坐标轴相切时,求G点的横坐标;
(3)过D点作直线DH∥AC交AB于H,当△DHF的面积最大时,在抛物线和直线AB上分别取M、N两点,并使D、H、M、N四点组成平行四边形,请你直接写出符合要求的M、N两点的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了求1+3+32+33+…+3100的值,可令M=1+3+32+33+…+3100 , 则3M=3+32+33+34+…+3101 , 因此,3M﹣M=3101﹣1,所以M= ![]() ,即1+3+32+33+…+3100=
,即1+3+32+33+…+3100= ![]() ,仿照以上推理计算:1+5+52+53+…+52015的值是 .
,仿照以上推理计算:1+5+52+53+…+52015的值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com