
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC=![]() ,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,则BE的长是 .
,将△ABC绕点A逆时针旋转60°,得到△ADE,连接BE,则BE的长是 .
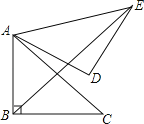
【答案】2+2![]()
【解析】
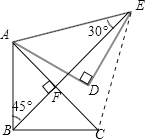
试题分析:首先考虑到BE所在的三角形并不是特殊三角形,所以猜想到要求BE,可能需要构造直角三角形.由旋转的性质可知,AC=AE,∠CAE=60°,故△ACE是等边三角形,可证明△ABE与△CBE全等,可得到∠ABE=45°,∠AEB=30°,再证△AFB和△AFE是直角三角形,然后在根据勾股定理求解
解:连结CE,设BE与AC相交于点F,如下图所示,
∵Rt△ABC中,AB=BC,∠ABC=90°
∴∠BCA=∠BAC=45°
∵Rt△ABC绕点A逆时针旋转60°与Rt△ADE重合,
∴∠BAC=∠DAE=45°,AC=AE
又∵旋转角为60°
∴∠BAD=∠CAE=60°,
∴△ACE是等边三角形
∴AC=CE=AE=4
在△ABE与△CBE中,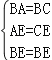
∴△ABE≌△CBE (SSS)
∴∠ABE=∠CBE=45°,∠CEB=∠AEB=30°
∴在△ABF中,∠BFA=180°﹣45°﹣45°=90°
∴∠AFB=∠AFE=90°
在Rt△ABF中,由勾股定理得,
BF=AF=![]() =2
=2
又在Rt△AFE中,∠AEF=30,°∠AFE=90°
FE=![]() AF=2
AF=2![]()
∴BE=BF+FE=2+2![]()
故,本题的答案是:2+2![]()


科目:初中数学 来源: 题型:
【题目】下列各式中去括号正确的是( )
A. a2-4(-a+1)= a2-4a﹣4 B. -(mn-1)+(m-n)=-mn-1+m-n
C. 5x-(2x-1)-x2= 5x-2x+1-x2 D. x2-2(2x-y+2)= x2-4x+y-2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年中秋、国庆假日八天里,中国民航共运送旅客1295万人次,将1295万用科学记数法表示应为( )
A. 0.1295 108 B. 1295104 C. 12.95 106 D. 1.295107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. 对角线相等的四边形是矩形B. 对角线互相垂直的四边形是正方形
C. 平行四边形的对角线平分一组对角D. 矩形的对角线相等且互相平分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
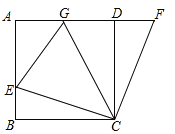
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com