Question

8．已知线段AB=10cm，直线AB上有一点C，BC=5cm，M是线段AB上的点，且AC：BM=3：1，求线段AM的长．

Answer 1

分析 根据线段的和差，可得AC的长，根据比例的性质，可得BM的长，再根据线段的和差，可得答案．

解答 解：①当C在线段AB的延长线上时，
如图1，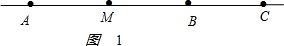
由线段的和差，得，
AC=AB+BC=10+5=15cm，
由比例的性质，得
BM=$\frac{1}{3}$AC=$\frac{1}{3}$×15=5cm．
由线段的和差，得
AM=AB-BM=15-5cm；
②当C在线段AB上时，AC=AB-BC=10-5=5cm，
如图2，
由比例的性质，得
BM=$\frac{1}{3}$AC=$\frac{1}{3}$×5=$\frac{5}{3}$cm．
由线段的和差，得
AM=AB-BM=10-$\frac{5}{3}$=$\frac{25}{3}$cm；
综上所述：线段AM的长5cm或$\frac{25}{3}$cm．

点评 本题考查了两点间的距离，利用比例的性质得出BM的长是解题关键，要分类讨论，以防遗漏．