
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为 . 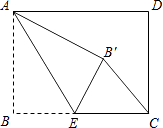
【答案】![]() 或3
或3
【解析】解:当△CEB′为直角三角形时,有两种情况: 
①当点B′落在矩形内部时,如答图1所示.
连结AC,
在Rt△ABC中,AB=3,BC=4,
∴AC= ![]() =5,
=5,
∵∠B沿AE折叠,使点B落在点B′处,
∴∠AB′E=∠B=90°,
当△CEB′为直角三角形时,只能得到∠EB′C=90°,
∴点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,
∴EB=EB′,AB=AB′=3,
∴CB′=5﹣3=2,
设BE=x,则EB′=x,CE=4﹣x,
在Rt△CEB′中,
∵EB′2+CB′2=CE2 ,
∴x2+22=(4﹣x)2 , 解得x= ![]() ,
,
∴BE= ![]() ;
;
②当点B′落在AD边上时,如答图2所示.
此时ABEB′为正方形,∴BE=AB=3.
综上所述,BE的长为 ![]() 或3.
或3.
故答案为: ![]() 或3.
或3.
当△CEB′为直角三角形时,有两种情况:①当点B′落在矩形内部时,如答图1所示.连结AC,先利用勾股定理计算出AC=5,根据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=3,可计算出CB′=2,设BE=x,则EB′=x,CE=4﹣x,然后在Rt△CEB′中运用勾股定理可计算出x.②当点B′落在AD边上时,如答图2所示.此时ABEB′为正方形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】老师计算学生的学期总评成绩按照如下的标准:平时作业占10%,单元测验占30%,期中考试占25%,期末考试占35%.小丽和小明的成绩如下所示:
学生 | 平时作业 | 单元测验 | 期中考试 | 期未考试 |
小丽 | 80 | 75 | 71 | 88 |
小明 | 76 | 80 | 70 | 90 |
请你通过计算,比较谁的学期总评成绩高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,∠B、∠C的平分线相交于点O,作BO、CO的垂直平分线分别交BC于点E、F.小明说:“E、F是BC的三等分点.”你同意他的说法吗?请说明理由.
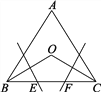
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:
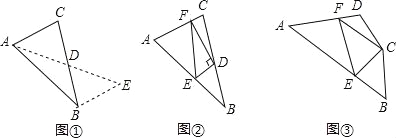
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从车站向东走400米,再向北走500米到小红家;从车站向北走500米,再向西走200米到小强家,则( )
A.小强家在小红家的正东
B.小强家在小红家的正西
C.小强家在小红家的正南
D.小强家在小红家的正北
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果经过三角形某一个顶点的一条直线可把它分成两个小等腰三角形,那么我们称该三角形为等腰三角形的生成三角形,简称生成三角形.
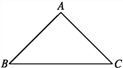
(1)如图,已知等腰直角三角形ABC,∠A=90°,试说明:△ABC是生成三角形;
(2)若等腰三角形DEF有一个内角等于36°,请你画出简图说明△DEF是生成三角形.(要求画出直线,标注出图中等腰三角形的顶角、底角的度数)
查看答案和解析>>
科目:初中数学 来源: 题型:
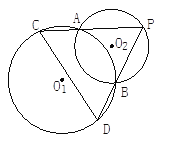
【题目】已知:如图,⊙O![]() 和⊙O
和⊙O![]() 相交于A、B两点, 动点P在⊙O
相交于A、B两点, 动点P在⊙O![]() 上,且在⊙
上,且在⊙![]() 外,直线PA、PB分别交⊙O
外,直线PA、PB分别交⊙O![]() 于C、D.问:⊙O
于C、D.问:⊙O![]() 的弦CD的长是否随点P的运动而发生变化?如果发生变化,请你确定CD最长和最短时P的位置,如果不发生变化,请你给出证明;
的弦CD的长是否随点P的运动而发生变化?如果发生变化,请你确定CD最长和最短时P的位置,如果不发生变化,请你给出证明;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com