
【题目】(1)阅读理解:
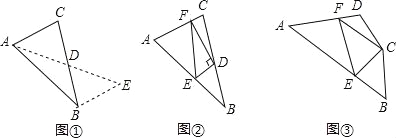
如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB、AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.中线AD的取值范围是 ;
(2)问题解决:
如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:
如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E、F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.
【答案】(1)2<AD<8;(2)证明详见解析;(3)BE+DF=EF;理由详见解析.
【解析】
试题分析:(1)延长AD至E,使DE=AD,由SAS证明△ACD≌△EBD,得出BE=AC=6,在△ABE中,由三角形的三边关系求出AE的取值范围,即可得出AD的取值范围;
(2)延长FD至点M,使DM=DF,连接BM、EM,同(1)得△BMD≌△CFD,得出BM=CF,由线段垂直平分线的性质得出EM=EF,在△BME中,由三角形的三边关系得出BE+BM>EM即可得出结论;
(3)延长AB至点N,使BN=DF,连接CN,证出∠NBC=∠D,由SAS证明△NBC≌△FDC,得出CN=CF,∠NCB=∠FCD,证出∠ECN=70°=∠ECF,再由SAS证明△NCE≌△FCE,得出EN=EF,即可得出结论.
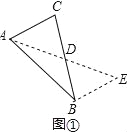
试题解析:(1)解:延长AD至E,使DE=AD,连接BE,如图①所示:
∵AD是BC边上的中线,
∴BD=CD,
在△BDE和△CDA中,BD=CD,∠BDE=∠CDA,DE=AD,
∴△BDE≌△CDA(SAS),
∴BE=AC=6,
在△ABE中,由三角形的三边关系得:AB﹣BE<AE<AB+BE,
∴10﹣6<AE<10+6,即4<AE<16,
∴2<AD<8;
故答案为:2<AD<8;
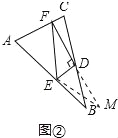
(2)证明:延长FD至点M,使DM=DF,连接BM、EM,如图②所示:
同(1)得:△BMD≌△CFD(SAS),
∴BM=CF,
∵DE⊥DF,DM=DF,
∴EM=EF,
在△BME中,由三角形的三边关系得:BE+BM>EM,
∴BE+CF>EF;
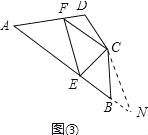
(3)解:BE+DF=EF;理由如下:
延长AB至点N,使BN=DF,连接CN,如图3所示:
∵∠ABC+∠D=180°,∠NBC+∠ABC=180°,
∴∠NBC=∠D,
在△NBC和△FDC中,
BN=DF,∠NBC =∠D,BC=DC,
∴△NBC≌△FDC(SAS),
∴CN=CF,∠NCB=∠FCD,
∵∠BCD=140°,∠ECF=70°,
∴∠BCE+∠FCD=70°,
∴∠ECN=70°=∠ECF,
在△NCE和△FCE中,
CN=CF,∠ECN=∠ECF,CE=CE,
∴△NCE≌△FCE(SAS),
∴EN=EF,
∵BE+BN=EN,
∴BE+DF=EF.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:初中数学 来源: 题型:
【题目】(1)已知4m=a,8n=b,用含a,b的式子表示下列代数式: ①求:22m+3n的值,
②求:24m﹣6n的值;
(2)已知2×8x×16=223,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD中,AE、AF分别是BC、CD的垂直平分线,∠EAF=80°,∠CBD=30°,则∠ADC的度数为( )

A. 45° B. 60°
C. 80° D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A关于x轴对称点的坐标为(2,-1),则点A的坐标为:( )
A. (-2,1) B. (2,1) C. (-2,-1) D. (-1,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为 . 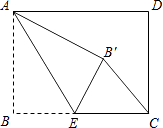
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中,装有2个白球和1个红球,这些球除颜色外其他都相同.
(1)小明认为,搅匀后从中任意摸出一个球,不是白球就是红球,因此摸出白球和摸出红球是等可能的.你同意他的说法吗?为什么?
(2)搅匀后从中摸出一个球,请求出不是白球的概率;
(3)搅匀后从中任意摸出一个球,要使摸出红球的概率为![]() ,应添加几个红球?
,应添加几个红球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当x=3时,整式px3+qx+1的值等于2012,那么当x=﹣3时,整式px3+qx+1的值为( )
A.2013
B.﹣2012
C.2014
D.﹣2010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场,顺风车行经营的A型车去年3月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年3月份与去年3月份卖出的A型车数量相同,则今年3月份A型车销售总额将比去年3月份销售总额增加25%.
(1)求今年3月份A型车每辆销售价多少元;
(2)该车行计划4月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A,B两种型号车的进货和销售价格表:
A型车 | B型车 | |
进货价格(元/辆) | 1100 | 1400 |
销售价格(元/辆) | 今年的销售价格 | 2400 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com