
分析 由次函数的定义可求得m的值,(1)当二次函数有最大值时,可知其开口向下,可求得相应的m的值,再根据其解析式可求得其最大值,利用增减性可求得答案;(2)由图象不经过第四象限可知其开口向上,可示得m的值,代入可求得其顶点坐标,再根据增减性可求得答案.
解答 解:
∵y=(m-1)x${\;}^{{m}^{2}-3m+2}$+mx+1是关于x的二次函数,
∴m2-3m+2=2,解得m=0或m=3,
(1)当二次函数有最大值时,则抛物线开口向下,
∴m=0,
∴抛物线解析式为y=-x2+1,
∴函数最大值为1,对称轴为y轴,
∴当x>0时,y随x的增大而减小;
(2)当二次函数的图象不经过第四象限时,则抛物线开口向上,
∴m=3,
∴y=2x2+3x+1=2(x+$\frac{3}{4}$)2-$\frac{1}{8}$,
∴抛物线顶点坐标为(-$\frac{3}{4}$,-$\frac{1}{8}$),对称轴为x=-$\frac{3}{4}$,
∴当x>-$\frac{3}{4}$时,y随x的增大而增大.
点评 本题主要考查二次函数的性质,由二次函数的定义求得m的值是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 12 | B. | 15 | C. | 12或15 | D. | 45 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
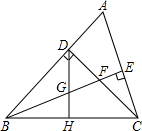 已知,如图△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G,有如下四个结论:①BF=AC;②CE=$\frac{1}{2}$BF;③CE>BG;④DG=DF;⑤连接DE,则∠DEB=45°,其中正确的有( )
已知,如图△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G,有如下四个结论:①BF=AC;②CE=$\frac{1}{2}$BF;③CE>BG;④DG=DF;⑤连接DE,则∠DEB=45°,其中正确的有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
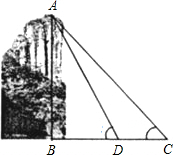 如图,为测得峰顶A到河面B的高度,当游船行至C处时测得峰顶A的仰角为45°,前进20米至D处时测得峰顶A的仰角为60°(此时C、D、B三点在同一直线上),求峰顶A到河面B的高度.(精确到0.1m,$\sqrt{2}$≈1.41,$\sqrt{3}$=1.73)
如图,为测得峰顶A到河面B的高度,当游船行至C处时测得峰顶A的仰角为45°,前进20米至D处时测得峰顶A的仰角为60°(此时C、D、B三点在同一直线上),求峰顶A到河面B的高度.(精确到0.1m,$\sqrt{2}$≈1.41,$\sqrt{3}$=1.73)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
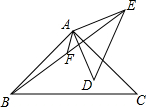 如图,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°,连接BE,F是BE的中点,连接AF.若AF=2,AD=5,tan∠DAF=$\frac{3}{4}$,则AB的边为$\frac{37\sqrt{5}}{5}$.
如图,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°,连接BE,F是BE的中点,连接AF.若AF=2,AD=5,tan∠DAF=$\frac{3}{4}$,则AB的边为$\frac{37\sqrt{5}}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com