
【题目】如图,以△ABC的BC边上一点O为圆心的圆,经过A、B两点,且与BC边交于点E,D为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.
(1)求证:AC是⊙O的切线:
(2)若BF=8,DF=![]() ,求⊙O的半径;
,求⊙O的半径;
(3)若∠ADB=60°,BD=1,求阴影部分的面积.(结果保留根号)

【答案】(1)证明见解析;(2)6;(3)![]() .
.
【解析】
(1)连接OA、OD,如图,利用垂径定理的推论得到OD⊥BE,再利用CA=CF得到
∠CAF= ∠CFA,然后利用角度的代换可证明∠OAD+∠CAF=![]() ,则OA⊥AC,从而根据
,则OA⊥AC,从而根据
切线的判定定理得到结论;
(2)设⊙0的半径为r,则OF=8-r,在Rt△ODF中利用勾股定理得到
![]() ,然后解方程即可;
,然后解方程即可;
(3)先证明△BOD为等腰直角三角形得到OB=![]() ,则OA=
,则OA=![]() ,再利用圆周角定理得到∠AOB=2∠ADB=
,再利用圆周角定理得到∠AOB=2∠ADB=![]() ,则∠AOE=
,则∠AOE=![]() ,接着在Rt△OAC中计算出AC,然后用一个直角三角形的面积减去一个扇形的面积去计算阴影部分的面积.
,接着在Rt△OAC中计算出AC,然后用一个直角三角形的面积减去一个扇形的面积去计算阴影部分的面积.
(1)证明:连接OA、OD,如图,
∵D为BE的下半圆弧的中点,
∴OD⊥BE,
∴∠ODF+∠OFD=90°,
∵CA=CF,
∴∠CAF=∠CFA,
而∠CFA=∠OFD,
∴∠ODF+∠CAF=90°,
∵OA=OD,
∴∠ODA=∠OAD,
∴∠OAD+∠CAF=90°,即∠OAC=90°,
∴OA⊥AC,
∴AC是⊙O的切线;
(2)解:设⊙O的半径为r,则OF=8﹣r,
在Rt△ODF中,(8﹣r)2+r2=(![]() )2,解得r1=6,r2=2(舍去),
)2,解得r1=6,r2=2(舍去),
即⊙O的半径为6;
(3)解:∵∠BOD=90°,OB=OD,
∴△BOD为等腰直角三角形,
∴OB=![]() BD=
BD=![]() ,
,
∴OA=![]() ,
,
∵∠AOB=2∠ADB=120°,
∴∠AOE=60°,
在Rt△OAC中,AC=![]() OA=
OA=![]() ,
,
∴阴影部分的面积=![]()
![]()
![]() ﹣
﹣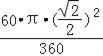 =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,小明家窗外有一堵围墙AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点C射进房间的地板F处,中午太阳光恰好能从窗户的最低点D射进房间的地板E处,小明测得窗子距地面的高度OD=0.8 m,窗高CD=1.2 m,并测得OE=0.8 m,OF=3 m,求围墙AB的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知长方形硬纸板ABCD的长BC为40cm,宽CD为30cm,按如图所示剪掉2个小正方形和2个小长方形(即图中阴影部分),将剩余部分折成一个有盖的长方体盒子,
设剪掉的小正方形边长为xcm.(纸板的厚度忽略不计)

(1)填空:EF= .cm,GH= .cm;(用含x的代数式表示)
(2)若折成的长方体盒子的表面积为950cm2,求该长方体盒子的体积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(![]() ,0),B(0,2),则点B2018的坐标为_____.
,0),B(0,2),则点B2018的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的解答过程,求y2+4y+8的最小值.解:y2+4y+8=y2+4y+4+4-(y+2)2+4,∵(y+2)2≥0,∴(y+2)2+4≥4,∴y2+4y+8的最小值为4.仿照上面的解答过程,求x2-x+4的最小值和6-2x-x2的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
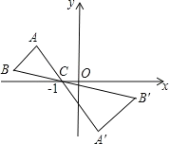
【题目】如图,△ABC中,A、B两个顶点在![]() 轴的上方,点C的坐标是(1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a,则点B的横坐标是( )
轴的上方,点C的坐标是(1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形,并把△ABC的边长放大到原来的2倍,设点B的对应点B′的横坐标是a,则点B的横坐标是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知点B的坐标为(6,4).
(1)请用直尺(不带刻度)和圆规作一条直线AC,它与x轴和y轴的正半轴分别交于点A和点C,且使∠ABC=90°,△ABC与△AOC的面积相等.(作图不必写作法,但要保留作图痕迹.)
(2)问:(1)中这样的直线AC是否唯一?若唯一,请说明理由;若不唯一,请在图中画出所有这样的直线AC,并写出与之对应的函数表达式.
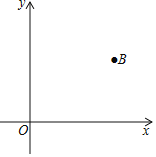
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船在A处测得灯塔P位于其东北方向上,轮船沿正东方向航行30海里到达B处后,此时测得灯塔P位于其北偏东30°方向上,此时轮船与灯塔P的距离是( )海里.

A. 15![]() +15 B. 30
+15 B. 30![]() +30 C. 45+15
+30 C. 45+15![]() D. 60
D. 60
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com