
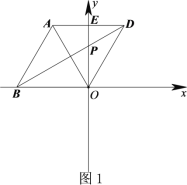
【题目】在平面直角坐标系xOy中,△![]() 为等边三角形,O为坐标原点,点A关于y轴的对称点为D,连接AD,BD,OD,其中AD,BD分别交y轴于点E,P.
为等边三角形,O为坐标原点,点A关于y轴的对称点为D,连接AD,BD,OD,其中AD,BD分别交y轴于点E,P.
(1)如图1,若点B在x轴的负半轴上时,直接写出![]() 的度数;
的度数;
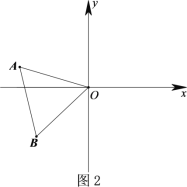
(2)如图2,将△![]() 绕点O旋转,且点A始终在第二象限,此时AO与y轴正半轴夹角为
绕点O旋转,且点A始终在第二象限,此时AO与y轴正半轴夹角为![]() ,60<
,60<![]() <90,依题意补全图形,并求出
<90,依题意补全图形,并求出![]() 的度数;(用含
的度数;(用含![]() 的式子表示)
的式子表示)
(3)在第(2)问的条件下,用等式表示线段BP,PE,PO之间的数量关系.(直接写出结果)
【答案】(1)30°;(2)作图见解析,∠BDO=α-60°;(3)2PE=BP+PO.
【解析】
(1)根据轴对称的性质和等边三角形的性质即可得出结论;
(2)由轴对称的性质和等边三角形的性质得出∠BOD=300°﹣2α.在△BOD中根据等腰三角形的性质和三角形内角和定理即可得出结论;
(3)过A作AQ∥EP交DB的延长线于Q,连接AP.由(2)得:∠OBD=∠BDO=α﹣60°.
通过证明△AOP≌△ABQ,得到AP=AQ,OP=QB,∠OAP=∠BAQ,BP+OP=BP+QB=QP.
通过证明△AQP是等边三角形,得出AQ=PQ=AP=BP+OP,∠QAP=60°,即可得到∠PAE=30°,由30°角所对直角边等于斜边的一半即可得到AP=2EP,从而得到结论.
(1)30°.理由如下:
∵A与D关于y轴对称,∴y轴是线段AD的垂直平分线,∴AO=DO,∠AOE=∠DOE.
∵△ABO是等边三角形,∴AB=BO=AO,∠AOB=60°,∴∠AOE=30°,∴∠DOE=30°,∴∠BOD=60°+30°+30°=120°.
∵BO=AO=DO,∴∠BDO=∠OBD=![]() (180°﹣∠BOD)=30°.
(180°﹣∠BOD)=30°.
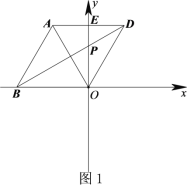
(2)正确画出图形.
∵∠AOE=∠DOE=α,∠AOB=60°,∴∠BOD=360°﹣2α﹣60°=300°﹣2α.
∵BO=BD,∴∠OBD=∠ODB,∴∠BDO=![]() (180°﹣∠BOD)=α﹣60°.
(180°﹣∠BOD)=α﹣60°.
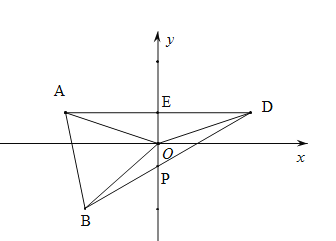
(3)2PE=BP+PO.理由如下:
过A作AQ∥EP交DB的延长线于Q,连接AP.由(2)得:∠OBD=∠BDO=α﹣60°.
∵△ABO是等边三角形,∴AB=BO=AO,∠ABO=∠AOB=∠BAO=60°,∴∠ABQ=180°﹣60°﹣∠OBD=120°﹣(α﹣60°)=180°﹣α.
∵∠AOE=α,∴∠AOP=180°﹣α,∴∠AOP=∠ABQ.
∵AQ∥EP,∴∠Q=∠EPD.
∵∠APE=∠DPE,∴∠APO=∠Q.
在△AOP和△ABQ中,∵∠AOP=∠ABQ,∠APO=∠Q,AO=AB,∴△AOP≌△ABQ,∴AP=AQ,OP=QB,∠OAP=∠BAQ,∴BP+OP=BP+QB=QP.
∵∠BAO=∠BAP+∠OAP=60°,∴∠BAP+∠BAQ=∠PAQ=60°.
∵AQ=AP,∴△AQP是等边三角形,∴AQ=PQ=AP=BP+OP.
∵AQ∥EP,∴∠APE=∠QAP=60°.
∵∠AEP=90°,∴∠PAE=30°,∴AP=2EP,∴2EP=BP+OP.


科目:初中数学 来源: 题型:
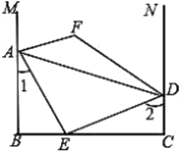
【题目】如图,![]() 平分
平分![]() 交
交![]() 于点
于点![]() 分别是
分别是![]() 延长线上的点,
延长线上的点,![]() 和
和![]() 的平分线交于点
的平分线交于点![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() 为定值.其中结论正确的有_______(填写所有正确的序号).
为定值.其中结论正确的有_______(填写所有正确的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
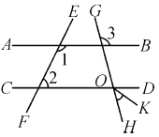
【题目】已知:如图,∠1+∠2=180°,∠3=100°,OK平分∠DOH.
(1)直线AB与CD有怎样的位置关系?说明理由;
(2)∠KOH的度数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】细观察,找规律
下列各图中的MA1与NAn平行.

(1)图①中的∠A1+∠A2= ______ 度,
图②中的∠A1+∠A2+∠A3= ______ 度,
图③中的∠A1+∠A2+∠A3+∠A4= ______ 度,
图④中的∠A1+∠A2+∠A3+∠A4+∠A5= ______ 度,
…,
第⑩个图中的∠A1+∠A2+∠A3+…+∠A11= ______ 度
(2)第n个图中的∠A1+∠A2+∠A3+…+∠An+1= ______
(3)请你证明图②的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据问题填空:
(1)问题发现:
如图①,在等边三角形ABC中,点M为BC边上异于B、C的一点,以AM为边作等边三角形AMN,连接CN,NC与AB的位置关系为;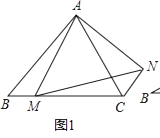
(2)深入探究:
如图②,在等腰三角形ABC中,BA=BC,点M为BC边上异于B、C的一点,以AM为边作等腰三角形AMN,使∠ABC=∠AMN,AM=MN,连接CN,试探究∠ABC与∠ACN的数量关系,并说明理由;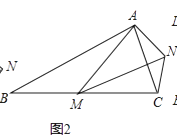
(3)拓展延伸:
如图③,在正方形ADBC中,AD=AC,点M为BC边上异于B、C的一点,以AM为边作正方形AMEF,点N为正方形AMEF的中点,连接CN,若BC=10,CN= ![]() ,试求EF的长.
,试求EF的长.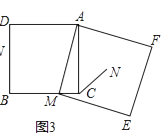
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.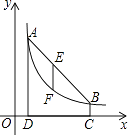
(1)求m,n的值并写出反比例函数的表达式;
(2)连接AB,E是线段AB上一点,过点E作x轴的垂线,交反比例函数图象于点F,若EF= ![]() AD,求出点E的坐标.
AD,求出点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别是R,S,若AQ=PQ,PR=PS,下面三个结沦:①AS=AR:②QP∥AR;③△BRP≌△CSP.其中正确的是( )
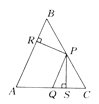
A. ①③ B. ②③ C. ①② D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,按以下步骤作图: 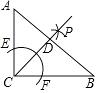
①以C为圆心,以适当长为半径画弧交AC于E,交BC于F.
②分别以E,F为圆心,以大于 ![]() EF的长为半径作弧,两弧相交于P;
EF的长为半径作弧,两弧相交于P;
③作射线CP交AB于点D,
若AC=3,BC=4,则△ACD的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com