
【题目】如图,在 ![]() 中,
中, ![]() 与
与 ![]() 的角平分线交于
的角平分线交于 ![]() 点.
点.
(1)若 ![]() ,则
,则 ![]()
![]() ;
;
(2)若 ![]() ,则
,则 ![]()
![]() ;
;
(3)若 ![]() ,
, ![]() 与
与 ![]() 的角平分线交于
的角平分线交于 ![]() 点,
点, ![]() 的平分线与
的平分线与 ![]() 的平分线交于点
的平分线交于点 ![]() ,
, ![]() ,
, ![]() 的平分线与
的平分线与 ![]() 的平分线交于点
的平分线交于点 ![]() ,则
,则 ![]()
![]() .
.
【答案】
(1)110
(2)(90 + ![]() n)
n)
(3)![]()
【解析】(1)∵∠A=40°,
∴∠ABC+∠ACB=140°,
∵点O是∠ABC与∠ACB的角平分线的交点,
∴∠OBC+∠OCB=70°,
∴∠BOC=110°。
故答案为:110°;
( 2 )∵∠A=n°,
∴∠ABC+∠ACB=180°-n°,
∵BO、CO分别是∠ABC与∠ACB的角平分线,
∴∠OBC+∠OCB= ![]() ∠ABC+
∠ABC+ ![]() ∠ACB
∠ACB
= ![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
= ![]() (180°-n°)
(180°-n°)
=90°- ![]() n°,
n°,
∴∠BOC=180°-(∠OBC+∠OCB)=90°+ ![]() n°.
n°.
故答案为:90°+ ![]() n°
n°
( 3 )由(2)得∠O=90°+ ![]() n°,
n°,
∵∠ABO的平分线与∠ACO的平分线交于点O1 ,
∴∠O1BC= ![]() ∠ABC,∠O1CB=
∠ABC,∠O1CB= ![]() ∠ACB,
∠ACB,
∴∠O1=180°- ![]() (∠ABC+∠ACB)=180°-
(∠ABC+∠ACB)=180°- ![]() (180°-∠A)=
(180°-∠A)= ![]() ×180°+
×180°+ ![]() n°,
n°,
同理,∠O2= ![]() ×180°+
×180°+ ![]() n°,
n°,
∴∠On= ![]() ×180°+
×180°+ ![]() °
°
∴∠O2017= ![]() °+
°+ ![]() n°,
n°,
故答案为: ![]() °+
°+ ![]() n°
n°
(1)根据三角形内角和定理和角平分线的性质,求出∠BOC的度数;(2)当∠A=n°时,由三角形内角和定理和角平分线的性质,得到∠BOC的代数式;(3)由(2)得∠O=90°+![]() n°,依次求出∠O1、∠O2···的代数式,得出结论.
n°,依次求出∠O1、∠O2···的代数式,得出结论.


科目:初中数学 来源: 题型:
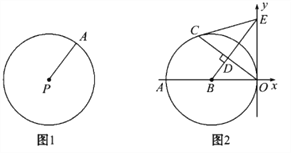
【题目】阅读下面材料:如图1,圆的概念:在平面内,线段PA绕它固定的一个端点P旋转一周,另一个端点A所形成的图形叫做圆.就是说,到某个定点等于定长的所有点在同一个圆上.圆心在P(a,b),半径为r的圆的方程可以写为:(x-a)2+(y-b)2=r2.如:圆心在P(2,-1),半径为5的圆的方程为:(x-2)2+(y+1)2=25.
(1)填空: ①以A(3,0)为圆心,1为半径的圆的方程为:________; ②以B(-1,-2)为圆心, ![]() 为半径的圆的方程为:________;
为半径的圆的方程为:________;
(2)根据以上材料解决以下问题:
如图2,以B(-6,0)为圆心的圆与y轴相切于原点,C是☉B上一点,连接OC,作BD⊥OC垂足为D,延长BD交y轴于点E,已知sin∠AOC=![]() .
.
①连接EC,证明EC是☉B的切线;
②在BE上是否存在一点P,使PB=PC=PE=PO,若存在,求P点坐标,并写出以P为圆心,以PB为半径的☉P的方程;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列 ![]() 个命题:其中真命题是( ).
个命题:其中真命题是( ).
⑴三角形的外角和是 ![]() ;⑵三角形的三个内角中至少有两个锐角;⑶直角三角形两锐角互余;⑷相等的角是对顶角.
;⑵三角形的三个内角中至少有两个锐角;⑶直角三角形两锐角互余;⑷相等的角是对顶角.
A.( ![]() )(
)( ![]() )
)
B.( ![]() )(
)( ![]() )
)
C.( ![]() )(
)( ![]() )
)
D.( ![]() )(
)( ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
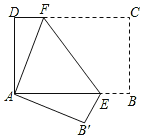
【题目】如图,将长方形纸片ABCD折叠,使点C与点A重合,折痕EF分别与AB、DC交于点E和点F.
(1)证明:△ADF≌△AB′E;
(2)若AD=12,DC=18,求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知坐标平面内的点A(-2,5),若将平面直角坐标系先向右平移3个单位长度,再向上平移4个单位长度,则点A在平移后的坐标系中的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD为菱形,点P为对角线BD上的一个动点.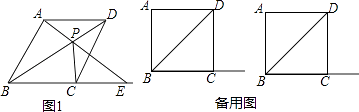
(1)如图1,连接AP并延长交BC的延长线于点E,连接 PC,求证:∠AEB=∠PCD.
(2)如图1,当PA=PD且PC⊥BE时,求∠ABC的度数.
(3)连接AP并延长交射线BC于点E,连接 PC,若∠ABC=90°且△PCE是等腰三角形,求∠PEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意解答
(1)探究:如图①,在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,AE⊥CD于点E,若AE=8,求四边形ABCD的面积. 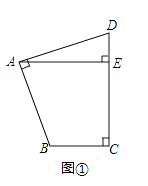
(2)应用:如图②,在四边形ABCD中,∠ABC+∠ADC=180°,AB=AD,AE⊥BC于点E,若AE=20,BC=10,CD=6,则四边形ABCD的面积为 . 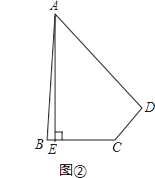
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com