
【题目】(1)问题发现
如图1,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,点D是线段AB上一动点,连接BE.
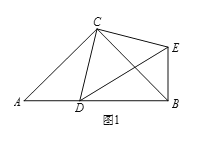
填空: ①![]() 的值为 ;②∠DBE的度数为 .
的值为 ;②∠DBE的度数为 .
(2)类比探究
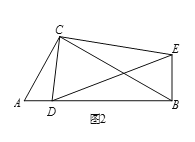
如图2,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,点D是线段AB上一动点,连接BE.请判断![]() 的值及∠DBE的度数,并说明理由.
的值及∠DBE的度数,并说明理由.
(3)拓展延伸
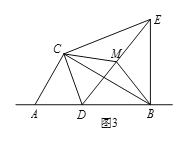
如面3,在(2)的条件下,将点D改为直线AB上一动点,其余条件不变,取线段DE的中点M,连接BM、CM,若AC=2,则当△CBM是直角三角形时,线段BE的长是多少?请直接写出答案.
【答案】(1)1,90°;(2)![]() ,90°,理由见解析;(3)3+
,90°,理由见解析;(3)3+![]() 或3-
或3-![]()
【解析】
(1)易得△ABC和△CDE为等腰直角三角形,所以AC=BC,CD=CE,通过证明△ACD≌△BCE,可得AD=BE和∠CAD=∠CBE=45°,进而得出答案;
(2)通过证明△ACD∽△BCE,可得![]() 的值,∠CBE=∠CAD=60°,即可求∠DBE的度数;
的值,∠CBE=∠CAD=60°,即可求∠DBE的度数;
(3)分点D在线段AB上和BA延长线上两种情况讨论,由直角三角形的性质可证CM=BM=![]() ,即可求DE=
,即可求DE=![]() ,由相似三角形的性质可得∠ABE=90°,BE=
,由相似三角形的性质可得∠ABE=90°,BE=![]() AD,由勾股定理可求BE的长.
AD,由勾股定理可求BE的长.
解:(1)∵∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,
∴∠ABC=∠CAB=45°,∠CDE=∠CED=45°
∴AC=BC,CD=CE
∵∠ACD+∠BCD=∠BCE+∠BCD=90°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
∵AC=BC,∠ACD=∠BCE,CD=CE
∴△ACD≌△BCE(SAS),
∴AD=BE,∠CAD=∠CBE=45°
∴![]() =1,∠DBE=∠ABC+∠CBE=90°
=1,∠DBE=∠ABC+∠CBE=90°
故答案为:1,90°;
(2)![]() =
=![]() ,∠DBE=90°,理由如下:
,∠DBE=90°,理由如下:
∵∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,
∴∠ACD=∠BCE,∠CED=∠ABC=30°,
∴tan∠ABC=tan30°=![]() =
=![]() .
.
∵∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,
∴Rt△ACB∽Rt△DCE,
∴![]() =
=![]() ,且∠ACD=∠BCE,
,且∠ACD=∠BCE,
∴△ACD∽△BCE,
∴![]() =
=![]() =
=![]() ,∠CBE=∠CAD=60°,
,∠CBE=∠CAD=60°,
∴∠DBE=∠ABC+∠CBE=90°;
(3)若点D在线段AB上,如图,
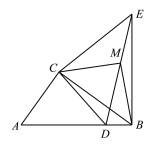
由(2)知:![]() =
=![]() =
=![]() ,∠ABE=90°,
,∠ABE=90°,
∴BE=![]() AD,
AD,
∵AC=2,∠ACB=90°,∠CAB=60°,
∴AB=4,BC=2![]() .
.
∵∠ECD=∠ABE=90°,且点M是DE中点,
∴CM=BM=![]() DE,
DE,
且△CBM是直角三角形,
∴CM2+BM2=BC2=(2![]() )2,
)2,
∴BM=CM=![]() ,
,
∴DE=2![]() ,
,
∵DB2+BE2=DE2,
∴(4-AD)2+(![]() AD)2=24,
AD)2=24,
∴AD=![]() +1,
+1,
∴BE=![]() AD=3+
AD=3+![]() ;
;
若点D在线段BA延长线上,如图,
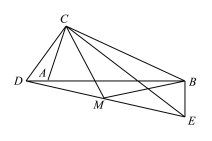
同理可得:DE=2![]() ,BE=
,BE=![]() AD,
AD,
∵BD2+BE2=DE2,
∴(4+AD)2+(![]() AD)2=24,
AD)2=24,
∴AD=![]() -1,
-1,
∴BE=![]() AD=3-
AD=3-![]() .
.
综上所述:BE的长为3+![]() 或3-
或3-![]() .
.


科目:初中数学 来源: 题型:
【题目】我国青少年的视力情况已受到全社会的广泛关注,某校随机调研了200名初中七、八、九年级学生的视力情况,并把调查数据绘制成以下统计图:
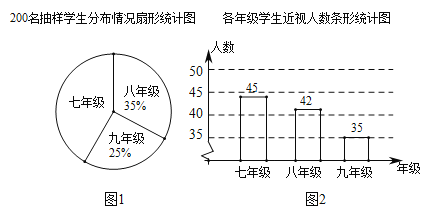
(1)七年级参加调查的有多少人?若该校有七年级学生500人,请估计七年级的近视人数;
(2)某同学说:“由图2可知,从七年级到九年级近视率越来越低.”你认为这种说法正确吗?请做判断,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.

(1)求证:△AEC≌△BED;
(2)若∠1=42°,求∠BDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
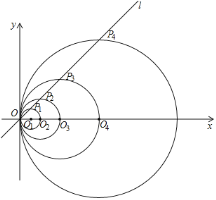
【题目】如图,在平面直角坐标系中,直线l的函数表达式为y=x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画圆,交直线l于点P1,交x轴正半轴于点O2;以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3;以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4;…按此做法进行下去,其中![]() 的长___________.
的长___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解班级学生数学课前预习的具体情况,郑老师对本班部分学生进行了为期一个月的跟踪调查,他将调查结果分为四类:A:很好;B:较好;C:一般;D:不达标,并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:

(1)C类女生有 名,D类男生有 名,将上面条形统计图补充完整;
(2)扇形统计图中“课前预习不达标”对应的圆心角度数是 ;
(3)为了共同进步,郑老师想从被调查的A类和D类学生中各随机机抽取一位同学进行“一帮一”互助学习,请用画树状图或列表的方法求出所选两位同学恰好是一男一女同学的概率,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点
经过点![]() ,且对称轴为直线
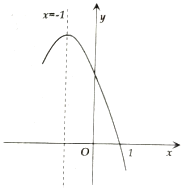
,且对称轴为直线![]() ,其部分图象如图所示对于此抛物线有如下四个结论:①
,其部分图象如图所示对于此抛物线有如下四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 若,则
若,则![]() 时的函数值小于
时的函数值小于![]() 时的函数值其中正确结论的个数是( )
时的函数值其中正确结论的个数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店计划购进一批甲、乙两种款式的运动服进行销售,进价和售价如下表所示:
运动服款式 | 甲 | 乙 |
进价(元/套) | 80 | 100 |
售价(元/套) | 120 | 160 |
若购进两种款式的运动服共300套,且投入资金不超过26800元.
(1) 该服装店应购进甲款运动服至少多少套?
(2)若服装店购进甲款运动服的进价每套降低a元,并保持这两款运动服的售价不变,且最多购进240套甲款运动服.如果这批运动服售出后,服装店刚好获利18480元,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ACB中,∠ACB=90°,CE是△ACB的中线,分别过点A、点C作CE和AB的平行线,交于点D.
(1)求证:四边形ADCE是菱形;
(2)若CE=4,且∠DAE=60°,求△ACB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com