练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】当三角形中的一个内角α是另一个内角β的一半时，我们称此三角形为“特征三角形”，其中α称为“特征角”．如果一个“特征三角形”的“特征角”为直角三角形，则这个“特征角”的度数为______．

    【答案】45°或30°

    【解析】

    分①“特征角”的2倍是直角时，根据“特征角”的定义列式计算即可得解；②“特征角”的2倍与“特征角”都不是直角，根据直角三角形两锐角互余列方程求解即可．

    解：①“特征角”的2倍是直角时，“特征角”=×90°=45°；

    ②“特征角”的2倍与“特征角”都不是直角时，设“特征角是x”，

    由题意得，x+2x=90°，

    解得x=30°，

    所以，“特征角”是30°，

    综上所述，这个“特征角”的度数为45°或30°．

    故答案为：45°或30°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（1）如图1，在矩形ABCD中，AB＝2，BC＝5，∠MPN＝90°，且∠MPN的直角顶点在BC边上，BP＝1．

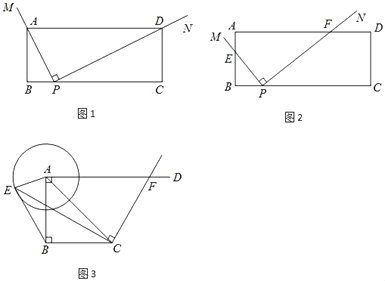
    ①特殊情形：若MP过点A，NP过点D，则＝　 　．

    ②类比探究：如图2，将∠MPN绕点P按逆时针方向旋转，使PM交AB边于点E，PN交AD边于点F，当点E与点B重合时，停止旋转．在旋转过程中，的值是否为定值？若是，请求出该定值；若不是，请说明理由．

    （2）拓展探究：在Rt△ABC中，∠ABC＝90°，AB＝BC＝2，AD⊥AB，⊙A的半径为1，点E是⊙A上一动点，CF⊥CE交AD于点F．请直接写出当△AEB为直角三角形时的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线与x轴、y轴分别交于A，B两点，C是OB的中点，D是AB上一点，四边形OEDC是菱形，则△OAE的面积为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题背景：在综合与实践课上，老师让同学们以“矩形纸片的剪拼”为主题开展数学活动．如图1：将矩形纸片ABCD沿对角线AC剪开，得到△ABC和△ACD．并且量AB＝4cm，AC＝8cm，问题解决：

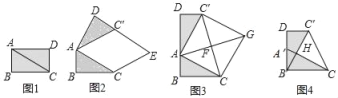
    （1）将图1中的△ACD以点为A旋转中心，按逆时针方向能转∠α，使∠α＝∠BAC，得到如图2所示的△AC'D，过点C作AC'的平行线，与DC'的延长线交于点E，则四边形ACEC'的形状是　 　．

    （2）缜密小组将图1中的△ACD以点A为旋转中心，按逆时针方向旋转，使B、A、D三点在同一条直线上，得到如图3所示的△AC'D，连接CC'，取CC'的中点F，连接AF并延长到点G，使FG＝AF，连接CG、C'G，得到四边形ACGC'，发现它是正方形，请你证明这个结论．

    实践探究：（3）创新小组在缜密小组发现结论的基础上，进行如下操作：将△ABC沿着BD方向平移，使点B与点A重合，此时A点平移至A'点，A'C与BC'相交于点H，如图4所示，连接CC'，试求tan∠C'CH的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：经过三角形一边中点，且平分三角形周长的直线叫做这个三角形在该边上的中分线，其中落在三角形内部的部分叫做中分线段．

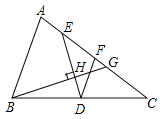
    （1）如图，△ABC中，AC＞AB，DE是△ABC在BC边上的中分线段，F为AC中点，过点B作DE的垂线交AC于点G，垂足为H，设AC＝b，AB＝c．

    ①求证：DF＝EF；

    ②若b＝6，c＝4，求CG的长度；

    （2）若题（1）中，S△BDH＝S△EGH，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2019年1月有300名教师参加了“新技术支持未来教育”培训活动，会议就“面向未来的教育”和“家庭教育”这两个问题随机调查了60位教师，并对数据进行了整理、描述和分析．下面给出了部分信息：

    a．关于“家庭教育”问题发言次数的频数分布直方图如下（数据分成6组：0≤x＜4，4≤x＜8，8≤x＜12，12≤x＜16，16≤x＜20，20≤x≤24）：

    b．关于“家庭教育”问题发言次数在8≤x＜12这一组的是：

    8899910101010101011111111

    c．“面向未来的教育”和“家庭教育”这两问题发言次数的平均数、众数、中位数如下：

    问题

    平均数

    中位数

    众数

    面向未来的学校教育

    11

    10

    9

    家庭教育

    12

    m

    10

    根据以上信息，回答下列问题：

    （1）表中m的值为______；

    （2）在此次采访中，参会教师更感兴趣的问题是______（填“面向未来的教育”或“家庭教育”），理由是______；

    （3）假设所有参会教师都接受调查，估计在“家庭教育”这个问题上发言次数超过8次的参会教师有______位．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

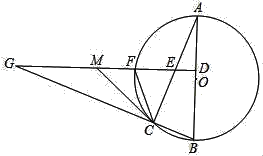
    【题目】如图，在⊙O中，AB为直径，AC为弦．过BC延长线上一点G，作GD⊥AO于点D，交AC于点E，交⊙O于点F，M是GE的中点，连接CF，CM．

    （1）判断CM与⊙O的位置关系，并说明理由；

    （2）若∠ECF=2∠A，CM=6，CF=4，求MF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

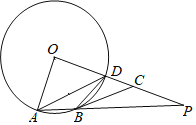
    【题目】如图，已知OA是⊙O的半径，AB为⊙O的弦，过点O作OP⊥OA，交AB的延长线上一点P，OP交⊙O于点D，连接AD，BD，过点B作⊙O的切线BC交OP于点C

    (1)求证：∠CBP＝∠ADB；

    (2)若O4＝4，AB＝2，求线段BP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

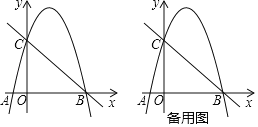
    【题目】如图，二次函数y＝ax2﹣3ax+c的图象与x轴交于点A、B，与y轴交于点C直线y＝﹣x+4经过点B、C．

    （1）求抛物线的表达式；

    （2）过点A的直线交抛物线于点M，交直线BC于点N．

    ①点N位于x轴上方时，是否存在这样的点M，使得AM：NM＝5：3？若存在，求出点M的坐标；若不存在，请说明理由．

    ②连接AC，当直线AM与直线BC的夹角∠ANB等于∠ACB的2倍时，请求出点M的横坐标．

    查看答案和解析>>

    同步练习册答案