
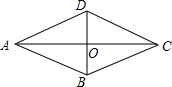
 一个菱形的一条对角线长60cm.周长是200cm.求:
一个菱形的一条对角线长60cm.周长是200cm.求:分析 (1)根据菱形四条边都相等求出边长,再根据菱形的对角线互相垂直平分,利用勾股定理列式求出另一对角线的一半,从而得到另一对角线的长度;
(2)根据菱形的面积等于对角线乘积的一半列式计算即可得解.
解答 解:∵菱形的周长是200cm,
∴菱形的边长为200÷4=50cm,
∵一条对角线长60cm,
∴该对角线的一半=60÷2=30cm,
∴另一对角线的一半=$\sqrt{5{0}^{2}-3{0}^{2}}$=40cm,
∴另一对角线长是40×2=80cm;
(2)由(1)可知这个菱形的面积=$\frac{1}{2}$×60×80=2400cm2.
点评 本题主要考查了菱形四条边都相等的性质,对角线互相垂直的性质,勾股定理的应用,熟记性质是解题的关键.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题
 如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.
如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| (a+b)1=a+b | 1 | 1 | ||||||||
| (a+b)2=a2+2ab+b2 | 1 | 2 | 1 | |||||||
| (a+b)3=a3+3a2b+3ab2+b3 | 1 | 3 | 3 | 1 | ||||||
| … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
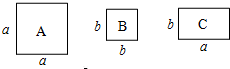 有若干张如图所示的正方形A类、B类卡片和长方形C类卡片,如果要拼成一个长为(2a+b),宽为(3a+2b)的大长方形,则需要C类卡片7张.
有若干张如图所示的正方形A类、B类卡片和长方形C类卡片,如果要拼成一个长为(2a+b),宽为(3a+2b)的大长方形,则需要C类卡片7张.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com