
分析 (1)根据等量关系“利润=(售价-进价)×销量”列出方程,解方程即可;
(2)设每件商品应降价y元,根据商场每天盈利300元列出方程,解方程即可.
解答 解:(1)设若商场想每天盈利225元,每件商品应降价x元,根据题意得
(10-x-8)(100+100x)=225,
解得:x1=x2=0.5.
答:商场想每天盈利225元,每件商品应降价0.5元.
(2)商场不能每天盈利300元,理由如下:
设若商场想每天盈利225元,每件商品应降价y元,根据题意得
(10-y-8)(100+100y)=300,
整理得y2-y+1=0,
∵△=1-4=-3<0,
∴y无实数根.
故商场不能每天盈利300元.
点评 此题考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
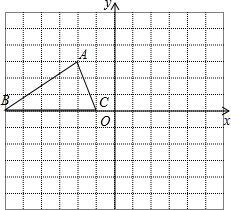 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(是弦的长)为37.4m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径.(精确到0.1m)
1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(是弦的长)为37.4m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径.(精确到0.1m)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com