
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
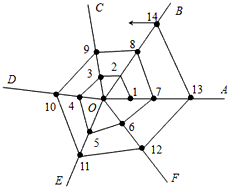 右图是蜘蛛结网过程示意图,一只蜘蛛先以O为起点结六条线OA,OB,OC,OD,OE,OF后,再从线OA上某点开始按逆时针方向依次在OA,BO,OC,OD,OE,OF,OA,OB,OF,OA,OB…上结网,若将各线上的结点依次记为1、2、3、4、5、6、7、8、…,那么第200个结点在OB条线段上.
右图是蜘蛛结网过程示意图,一只蜘蛛先以O为起点结六条线OA,OB,OC,OD,OE,OF后,再从线OA上某点开始按逆时针方向依次在OA,BO,OC,OD,OE,OF,OA,OB,OF,OA,OB…上结网,若将各线上的结点依次记为1、2、3、4、5、6、7、8、…,那么第200个结点在OB条线段上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
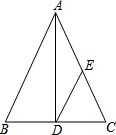 如图,已知在△ABC中,AB=AC,AD是BC边上的高线,DE∥AB交AC于点E,猜想DE与AB的数量关系,并证明你的猜想.
如图,已知在△ABC中,AB=AC,AD是BC边上的高线,DE∥AB交AC于点E,猜想DE与AB的数量关系,并证明你的猜想.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com