
【题目】张师傅准备用长为8cm的铜丝剪成两段,以围成两个正方形的线圈,设剪成的两段铜丝中的一段的长为xcm,围成的两个正方形的面积之和为Scm2 .
(1)求S与x的函数关系式,并写出自变量的取值范围;
(2)当x取何值时,S取得最小值,并求出这个最小值.
【答案】
(1)解:设一段铁丝的长度为x,另一段为(8﹣x),则边长分别为 ![]() x,
x, ![]() (8﹣x),
(8﹣x),
则S= ![]() x2+
x2+ ![]() (8﹣x)(8﹣x)=
(8﹣x)(8﹣x)= ![]() x2﹣x+4;自变量的取值范围:0<x<8
x2﹣x+4;自变量的取值范围:0<x<8
(2)解:S= ![]() (x﹣4)2+2,
(x﹣4)2+2,
所以当x=4cm时,S最小,最小为2cm2
【解析】(1)设一段铁丝的长度为x,另一段为(8﹣x),则边长分别为 ![]() x,
x, ![]() (8﹣x),然后根据正方形的面积公式及S=一个正方形的面积+另一个正方形的面积,列出函数关系式,直接根据实际情况写出自变量的取值范围;
(8﹣x),然后根据正方形的面积公式及S=一个正方形的面积+另一个正方形的面积,列出函数关系式,直接根据实际情况写出自变量的取值范围;
(2)将(1)中得到的函数关系式化为顶点式,由于该函数图像的开口向上,根据顶点坐标得出当x=4cm时,S最小,最小为2cm2。
【考点精析】掌握二次函数的最值是解答本题的根本,需要知道如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:
【题目】 如图,数轴上点A对应的有理数为10,点P以每秒1个单位长度的速度从点A出发,点Q以每秒3个单位长度的速度从原点O出发,且P、Q两点同时向数轴正方向运动,设运动时间为t秒.
(1)当t=2时,P,Q两点对应的有理数分別是 , ,PQ= ;
(2)当PQ=8时,求t的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
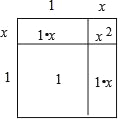
【题目】(1)下面是李老师带领同学们探索![]() 的近似值的过程,请你仔细阅读并补充完整:我们知道,面积是2的正方形的边长是
的近似值的过程,请你仔细阅读并补充完整:我们知道,面积是2的正方形的边长是![]() ,且
,且![]() >1,则设
>1,则设![]() =1+x(0<x<1),可画出如图所示的示意图.由各部分面积之和等于总面积.可列方程为:x2+ +1=2,∵0<x<1,∴认为x2是个较为接近于0的数,令x2≈0,因此省略x2后,得到方程: ,解得,x= ,即
=1+x(0<x<1),可画出如图所示的示意图.由各部分面积之和等于总面积.可列方程为:x2+ +1=2,∵0<x<1,∴认为x2是个较为接近于0的数,令x2≈0,因此省略x2后,得到方程: ,解得,x= ,即![]() =1+x≈ .
=1+x≈ .
(2)请仿照(1)中的方法,若设![]() =1.7+y(0<y<1),求
=1.7+y(0<y<1),求![]() 的近似值(要求画出示意图,标明数据,并将
的近似值(要求画出示意图,标明数据,并将![]() 的近似值精确到千分位)
的近似值精确到千分位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的线段AB及点P,给出如下定义:
若点P满足PA=PB,则称P为线段AB的“轴点”,其中,当0°<∠APB<60°时,称P为线段AB的“远轴点”;当60°≤∠APB≤180°时,称P为线段AB的“近轴点”.
(1)如图1,点A,B的坐标分别为(-2,0),(2,0),则在![]() ,
,![]() ,
,![]() ,
,![]() 中,线段AB的“近轴点”是 .
中,线段AB的“近轴点”是 .
(2)如图2,点A的坐标为(3,0),点B在y轴正半轴上,且∠OAB=30°.
①若P为线段AB的“远轴点”,直接写出点P的横坐标t的取值范围 ;
②点C为y轴上的动点(不与点B重合且BC≠AB),若Q为线段AB的“轴点”,当线段QB与QC的和最小时,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上一点,OD平分∠BOC,OE平分∠AOC,则下列说法错误的是( )

A. ∠DOE为直角B. ∠DOC和∠AOE互余
C. ∠AOD和∠DOC互补D. ∠AOE和∠BOC互补
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算并观察下列各式:
第1个:(a﹣b)(a+b)=______;
第2个:(a﹣b)(a2+ab+b2)=______;
第3个:(a﹣b)(a3+a2b+ab2+b3)=_______;
……
这些等式反映出多项式乘法的某种运算规律.
(2)猜想:若n为大于1的正整数,则(a﹣b)(an﹣1+an﹣2b+an﹣3b2+……+a2bn﹣3+abn﹣2+bn﹣1)=________;
(3)利用(2)的猜想计算:2n﹣1+2n﹣2+2n﹣3+……+23+22+1=______.
(4)拓广与应用:3n﹣1+3n﹣2+3n﹣3+……+33+32+1=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为深化课程改革,某校为学生开设了形式多样的社团课程,为了解部分社团课程在学生中最受欢迎的程度,学校随机抽取七年级![]() 名学生进行调查,从
名学生进行调查,从![]() :文学鉴赏,
:文学鉴赏,![]() :科学探究,
:科学探究,![]() :文史天地,
:文史天地,![]() :趣味数学四门课程中选出你喜欢的课程(被调查的每名学生必选且只能选择一门课程),并将调查结果制成如下两幅不完整的统计图:
:趣味数学四门课程中选出你喜欢的课程(被调查的每名学生必选且只能选择一门课程),并将调查结果制成如下两幅不完整的统计图:

(1)![]() _________,
_________,![]() _________;
_________;
(2)扇形统计图中,“![]() ”所对应的扇形的圆心角度数是________度;
”所对应的扇形的圆心角度数是________度;
(3)请根据以上信息直接在答题卡中补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红根据学习“数与式”积累的经验,想通过“由特殊到一般”的方法探究下面二次根式的运算规律.
下面是小红的探究过程,请补充完整:
(1)具体运算,发现规律.
特例1:![]() ,
,
特例2:![]() ,
,
特例3:![]() ,
,
特例4: (填写一个符合上述运算特征的例子).
(2)观察、归纳,得出猜想.
如果![]() 为正整数,用含
为正整数,用含![]() 的式子表示上述的运算规律为: .
的式子表示上述的运算规律为: .
(3)证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了预测本校应届毕业女生“一分钟跳绳”项目考试情况,从九年级随机抽取部分女生进行该项目测试,并以测试数据为样本,绘制出如图所示的部分频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值)和扇形统计图.根据统计图提供的信息解答下列问题: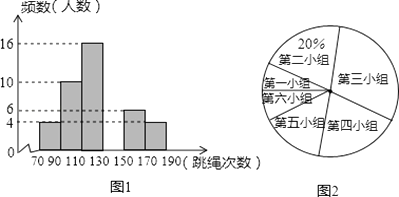
(1)补全频数分布直方图 , 并指出这个样本数据的中位数落在第小组;(1)
(2)若测试九年级女生“一分钟跳绳”次数不低于130次的成绩为优秀,本校九年级女生共有260人,请估计该校九年级女生“一分钟跳绳”成绩为优秀的人数;
(3)如测试九年级女生“一分钟跳绳”次数不低于170次的成绩为满分,在这个样本中,从成绩为优秀的女生中任选一人,她的成绩为满分的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com