
【题目】如图,O是直线AB上一点,OD平分∠BOC,OE平分∠AOC,则下列说法错误的是( )

A. ∠DOE为直角B. ∠DOC和∠AOE互余
C. ∠AOD和∠DOC互补D. ∠AOE和∠BOC互补
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
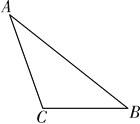
【题目】如图,在△ABC中,∠B=38°,∠C=112°.(1)按下列要求作图:(保留作图痕迹)
①BC边上的高AD;
②∠A的平分线AE.
(2)求∠DAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)图1中阴影部分面积为______,图2中阴影部分面积为_____,对照两个图形的面积可以验证________公式(填公式名称)请写出这个乘法公式________.
(2)应用(1)中的公式,完成下列各题:
①已知x2﹣4y2=15,x+2y=3,求x﹣2y的值;
②计算:(2+1)(22+1)(24+1)(28+1)……(264+1)+1.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABO.
(1)点A关于x轴对称的点的坐标为_________,点B关于y轴对称的点的坐标为_________;
(2)判断△ABO的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张师傅准备用长为8cm的铜丝剪成两段,以围成两个正方形的线圈,设剪成的两段铜丝中的一段的长为xcm,围成的两个正方形的面积之和为Scm2 .
(1)求S与x的函数关系式,并写出自变量的取值范围;
(2)当x取何值时,S取得最小值,并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.如果一条直线与果圆只有一个交点,则这条直线叫做果圆的切线.已知A、B、C、D四点为果圆与坐标轴的交点,E为半圆的圆心,抛物线的解析式为y=x2﹣2x﹣3,AC为半圆的直径.
(1)分别求出A、B、C、D四点的坐标;
(2)求经过点D的果圆的切线DF的解析式;
(3)若经过点B的果圆的切线与x轴交于点M,求△OBM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球每筒的售价多15元,小彬从该网店购买了3筒甲种羽毛球和2筒乙种羽毛球,一共花费270元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据消费者需求,该网店决定购进甲、乙两种羽毛球各80筒.已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.元旦期间该网店开展优惠促销活动,甲种羽毛球打折销售,乙种羽毛球售价不变,若所购进羽毛球均可全部售出,要使全部售出所购进的羽毛球的利润率是![]() ,那么甲种羽毛球是按原销售价打几折销售的.
,那么甲种羽毛球是按原销售价打几折销售的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,正比例函数 ![]() 的图象与反比例函数
的图象与反比例函数 ![]()
![]() 在第一象限的图象交于点
在第一象限的图象交于点 ![]() ,过点
,过点 ![]() 作
作 ![]() 轴的垂线,垂足为
轴的垂线,垂足为 ![]() ,已知△OAM的面积为1.
,已知△OAM的面积为1.
(1)求反比例函数的解析式;
(2)如果点 ![]() 为反比例函数在第一象限图象上的点(点
为反比例函数在第一象限图象上的点(点 ![]() 与点
与点 ![]() 不重合),且点
不重合),且点 ![]() 的横坐标为1,在
的横坐标为1,在 ![]() 轴上求一点
轴上求一点 ![]() ,使
,使 ![]() 最小.
最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com