
����Ŀ����ͼ�����ǰ�һ����Բ�������ߵ�һ����Χ�ɵķ��ͼ�γ�Ϊ����Բ�������һ��ֱ�����Բֻ��һ�����㣬������ֱ�߽�����Բ�����ߣ���֪A��B��C��D�ĵ�Ϊ��Բ��������Ľ��㣬EΪ��Բ��Բ�ģ������ߵĽ���ʽΪy=x2��2x��3��ACΪ��Բ��ֱ����
��1���ֱ����A��B��C��D�ĵ�����ꣻ
��2������D�Ĺ�Բ������DF�Ľ���ʽ��
��3����������B�Ĺ�Բ��������x�ύ�ڵ�M�����OBM�������
���𰸡�
��1���⣺����DE�� 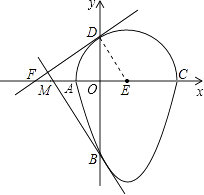
��y=x2��2x��3��
��x=0ʱ��y=��3��
y=0ʱ��x1=��1��x2=3��
���A����������1��0������B��������0����3������C��������3��0����
��AC=4��
��AE=DE=2��
��OE=1��
��OD= ![]() =
= ![]() ��
��
��D���������0�� ![]() ��
��
��2���⣺��DF�ǹ�Բ�����ߣ�
��ED��DF����DO��EF��
��DE2=EOEF��
��EF=4����OF=3��
���F����������3��0����
�辭����D�Ĺ�Բ������DF�Ľ���ʽΪy=kx+b��
�� ![]() ��
��
��� 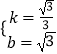 ��
��
�ྭ����D�Ĺ�Բ������DF�Ľ���ʽΪy= ![]() x+
x+ ![]()
��3���⣺�辭����B�Ĺ�Բ�����ߵĽ���ʽΪ��y=ax+c��
�ߵ�B������Ϊ��0����3����
�ྭ����B�Ĺ�Բ�����ߵĽ���ʽΪ��y=ax��3��
������ã������� ![]() ֻ��һ���⣬
ֻ��һ���⣬
��һԪ���η���x2����a+2��x=0��������ȵ�ʵ������
��=��a+2��2��4��1��0=0��
���a=��2��
�ྭ����B�Ĺ�Բ�����ߵĽ���ʽΪ��y=��2x��3��
��y=0ʱ��x=�� ![]() ��
��
���M���������� ![]() ��0������OM=
��0������OM= ![]() ��
��
���OBM�����= ![]() ��OM��OB=
��OM��OB= ![]() ��
��
����������1������DE�� �����������ϵ�������ص����A,B,C��������꣬����A,C��������������Բֱ��AC�ij����Ӷ��ó��뾶AE=DE=2�����OE�ij������ݹ��ɶ����ó�OD�ij����Ӷ��ó�D������ꣻ
��2���������ߵ����ʵó�ED��DF����DO��EF���Ӷ��жϳ���OED![]() ��DEF,�������������ζ�Ӧ�߳ɱ����ó�DE2=EOEF���Ӷ��ó���F�����꣬�辭����D�Ĺ�Բ������DF�Ľ���ʽΪy=kx+b���ô���ϵ�������������D�Ĺ�Բ������DF�Ľ���ʽ��
��DEF,�������������ζ�Ӧ�߳ɱ����ó�DE2=EOEF���Ӷ��ó���F�����꣬�辭����D�Ĺ�Բ������DF�Ľ���ʽΪy=kx+b���ô���ϵ�������������D�Ĺ�Բ������DF�Ľ���ʽ��
��3���辭����B�Ĺ�Բ�����ߵĽ���ʽΪ��y=ax+c������ֱ�߹���B���ʾ�����B�Ĺ�Բ�����ߵĽ���ʽΪ��y=ax��3������y=ax��3��y=x2��2x��3��ɵķ�����ֻ��һ���⣬��һԪ���η���x2����a+2��x=0��������ȵ�ʵ�������ɸ����б�ʽ��a+2��2��4��1��0=0���ó�a��ֵ���Ӷ��ó�������B�Ĺ�Բ�����ߵĽ���ʽΪ��y=��2x��3�������ҵ�M������꣬�����OBM�������
�����㾫����������Ĺؼ��������������ε���������֪ʶ�����������ε����=1/2���ס��ߣ��Լ������������ε��ж������ʵ����⣬�˽����������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��D��E�ֱ���������ABC�ı�AB��BC�ϵĵ㣬DE��AC����F��DE���ӳ����ϣ��ҡ�DFC����A��
��1����֤��AB��CF��
��2������ACF�ȡ�BDE��40�㣬���BDE�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
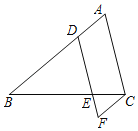
����Ŀ����ͼ��AB��CD����A��50������C��45�������P�Ķ�����
�����ṩ����˼·��
(1)��P��FG��AB
(2)�ӳ�AP��ֱ��CD��M��
(3)�ӳ�CP��ֱ��AB��N��
��ѡ������˼·�������P�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��O��ֱ��AB��һ�㣬ODƽ�֡�BOC��OEƽ�֡�AOC��������˵��������ǣ� ��

A. ��DOEΪֱ��B. ��DOC�͡�AOE����
C. ��AOD�͡�DOC����D. ��AOE�͡�BOC����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��γ���ѧ�����������������������������������±����˱���ʾ��(nΪ�Ǹ�����)չ��ʽ�ĸ���ϵ���Ĺ��ɣ����磺
(a+b)0��1����ֻ��һ�ϵ��Ϊ1��
(a+b)1��a+b���������ϵ���ֱ�Ϊ1��1��
(a+b)2��a2+2ab+b2���������ϵ���ֱ�Ϊ1��2��1��
(a+b)3��a3+3a2b+3ab2+b3���������ϵ���ֱ�Ϊ1��3��3��1����
�������Ϲ��ɣ�(a+b)6չ��ʽ����______�����ϵ���ĺ͵���______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��γ̸ĸijУΪѧ����������ʽ���������ſγ̣�Ϊ�˽ⲿ�����ſγ���ѧ�������ܻ�ӭ�ij̶ȣ�ѧУ�����ȡ���꼶![]() ��ѧ�����е��飬��
��ѧ�����е��飬��![]() ����ѧ���ͣ�
����ѧ���ͣ�![]() ����ѧ̽����
����ѧ̽����![]() ����ʷ��أ�
����ʷ��أ�![]() ��Ȥζ��ѧ���ſγ���ѡ����ϲ���Ŀγ̣��������ÿ��ѧ����ѡ��ֻ��ѡ��һ�ſγ̣��������������Ƴ�����������������ͳ��ͼ��
��Ȥζ��ѧ���ſγ���ѡ����ϲ���Ŀγ̣��������ÿ��ѧ����ѡ��ֻ��ѡ��һ�ſγ̣��������������Ƴ�����������������ͳ��ͼ��

��1��![]() _________��
_________��![]() _________��
_________��
��2������ͳ��ͼ�У���![]() ������Ӧ�����ε�Բ�ĽǶ�����________�ȣ�
������Ӧ�����ε�Բ�ĽǶ�����________�ȣ�
��3�������������Ϣֱ���ڴ���в�ȫ����ͳ��ͼ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ֱ��û���������������κ������Σ�������ֻ��һ������.
![]()
��1�������![]() ����������Ҫ����________���������
����������Ҫ����________���������![]() ����������Ҫ����________����
����������Ҫ����________����
��2������������κ������ι�����2018���������������εĸ����������εĸ�����3���������������θ�����________�������εĵĸ�����________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=�� ![]() +bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C���ҡ�BAC=������ABC=
+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C���ҡ�BAC=������ABC= ![]() ��tan����tan��=2����ACB=90�㣮
��tan����tan��=2����ACB=90�㣮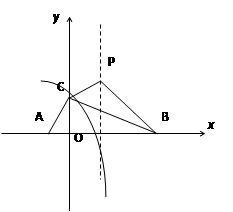
��1�����C�����ꣻ
��2���������ߵĽ���ʽ��
��3���������ߵĶ���ΪP�����ı���ABPC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����5��д�Ų�ͬ�����ֵĿ�Ƭ�����㰴Ҫ������Ƭ��������и����⣺
![]()
��1������ȡ��2�ſ�Ƭ��ʹ��2�ſ�Ƭ�����ֳ˻�������ֵ���� ����
��2������ȡ��2�ſ�Ƭ��ʹ��2�ſ�Ƭ���������������С����Сֵ���� ����
��3������ȡ��4�ſ�Ƭ����ѧ�������㷽����ʹ���Ϊ24��д������ʽ�ӣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com