
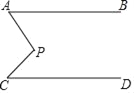
【题目】如图,AB∥CD,∠A=50°,∠C=45°,求∠P的度数.
下面提供三种思路:
(1)过P作FG∥AB
(2)延长AP交直线CD于M;
(3)延长CP交直线AB于N.
请选择两种思路,求出∠P的度数.
【答案】∠APC=95°,方法见解析.
【解析】
(1)过P作PG∥AB,利用平行线的性质以及三角形外角性质进行计算即可.
(2)延长AP交直线CD于M,利用平行线的性质以及三角形外角性质进行计算即可.
(3)延长CP交直线AB于N,利用平行线的性质以及三角形外角性质进行计算即可.
解:(1)过P作PG∥AB,
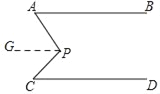
∵AB∥CD,
∴AB∥CD∥PG,
∴∠A=∠APG,∠C=∠CPG,
∴∠APC=APG+∠CPG=∠A+∠C=50°+45°=95°;
(2)延长AP交直线CD于M;
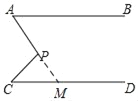
∵AB∥CD,
∴∠A=∠AMC=50°,
又∵∠C=45°,
∴∠APC=∠AMC+∠C=50°+45°=95°;
(3)延长CP交直线AB于N.
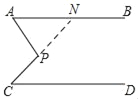
∵AB∥CD,
∴∠C=∠ANC=45°,
又∵∠A=50°,
∴∠APC=∠ANC+∠A=45°+50°=95°.


科目:初中数学 来源: 题型:
【题目】小明是个爱动脑筋的学生,在学习了解直角三角形以后,一天他去测量学校的旗杆DF的高度,此时过旗杆的顶点F的阳光刚好过身高DE为1.6米的小明的头顶且在他身后形成的影长DC=2米.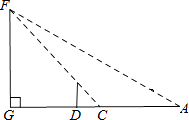
(1)若旗杆的高度FG是a米,用含a的代数式表示DG.
(2)小明从点C后退6米在A的测得旗杆顶点F的仰角为30°,求旗杆FG的高度.(点A、C、D、G在一条直线上, ![]() ,结果精确到0.1)
,结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠BAC=∠ABD=90°,AC=BD,点O是AD,BC的交点,点E是AB的中点.
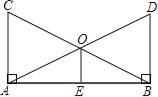
(1)图中有哪几对全等三角形?请写出来;
(2)试判断OE和AB的位置关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,D在BC的延长线上,∠ABC与∠ACD的平分线相交于点P,则下列结论中不一定正确的是( )
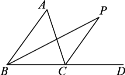
A. ∠ACD=2∠A B. ∠A=2∠P C. BP⊥AC D. BC=CP
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)图1中阴影部分面积为______,图2中阴影部分面积为_____,对照两个图形的面积可以验证________公式(填公式名称)请写出这个乘法公式________.
(2)应用(1)中的公式,完成下列各题:
①已知x2﹣4y2=15,x+2y=3,求x﹣2y的值;
②计算:(2+1)(22+1)(24+1)(28+1)……(264+1)+1.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABO.
(1)点A关于x轴对称的点的坐标为_________,点B关于y轴对称的点的坐标为_________;
(2)判断△ABO的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.如果一条直线与果圆只有一个交点,则这条直线叫做果圆的切线.已知A、B、C、D四点为果圆与坐标轴的交点,E为半圆的圆心,抛物线的解析式为y=x2﹣2x﹣3,AC为半圆的直径.
(1)分别求出A、B、C、D四点的坐标;
(2)求经过点D的果圆的切线DF的解析式;
(3)若经过点B的果圆的切线与x轴交于点M,求△OBM的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时![]() 张用A方法,其余用B方法。
张用A方法,其余用B方法。
(1)用![]() 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com