
【题目】若关于x的一元二次方程4x2+4(a﹣1)x+a2﹣a﹣2=0没有实数根.
(1)求实数a的取值范围;
(2)化简: ![]() ﹣
﹣ ![]() .
.
【答案】
(1)解:∵关于x的一元二次方程4x2+4(a﹣1)x+a2﹣a﹣2=0没有实数根,
∴△=16(a﹣1)2﹣4×4(a2﹣a﹣2)<0,
即﹣16a+48<0,
解得a>3
(2)解:∵原式= ![]() ﹣
﹣ ![]() =
= ![]() =|3﹣a|﹣|a+6|,
=|3﹣a|﹣|a+6|,
=|3﹣a|﹣|a+6|,
=a﹣3﹣(a+6),
=﹣9.
【解析】根据根的判别式知:关于x的一元二次方程4x2+4(a﹣1)x+a2﹣a﹣2=0没有实数根,故得出不等式16(a﹣1)2﹣4×4(a2﹣a﹣2)<0,求解即可得出a的取值范围;
(2)根据完全平方公式将被开方数写成一个式子的完全平方,然后根据一个数的平方的算数平方根等于它的 绝对值,再根据(1)小题得出的a的取值范围判断出绝对值里面部分的正负,再根据绝对值的意义去掉绝对值符号,再合并同类项即可。
【考点精析】利用二次根式的性质与化简和求根公式对题目进行判断即可得到答案,需要熟知1、如果被开方数是分数(包括小数)或分式,先利用商的算数平方根的性质把它写成分式的形式,然后利用分母有理化进行化简.2、如果被开方数是整数或整式,先将他们分解因数或因式,然后把能开得尽方的因数或因式开出来;根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的两条边在坐标轴上,OA=1,OC=2,现将此矩形向右平移,每次平移1个单位,若第1次平移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,则第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为(用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
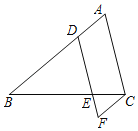
【题目】如图,D,E分别是三角形ABC的边AB,BC上的点,DE∥AC,点F在DE的延长线上,且∠DFC=∠A.
(1)求证:AB∥CF;
(2)若∠ACF比∠BDE大40°,求∠BDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将直角三角形ABC绕其直角顶点C顺时针旋转至△A′B′C′,已知AC=8,BC=6,点M,M′分别是AB,A′B′的中点,则MM′的长是( )

A. 5![]() B. 4 C. 3 D. 5
B. 4 C. 3 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
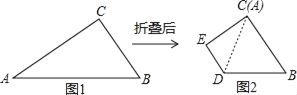
【题目】如图①,△ABC中,∠ACB=90°,AC=3![]() ,BC=3,如图②,将△ABC沿一条直线折叠,使得点A与点C重合
,BC=3,如图②,将△ABC沿一条直线折叠,使得点A与点C重合
(1)在图①中画出折痕所在的直线l,设直线l与AB,AC分别相交于点D,E(尺规作图,不写作法,保留作图痕迹)
(2)如图②,求△CDB的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)下面是李老师带领同学们探索![]() 的近似值的过程,请你仔细阅读并补充完整:我们知道,面积是2的正方形的边长是
的近似值的过程,请你仔细阅读并补充完整:我们知道,面积是2的正方形的边长是![]() ,且
,且![]() >1,则设
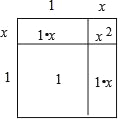
>1,则设![]() =1+x(0<x<1),可画出如图所示的示意图.由各部分面积之和等于总面积.可列方程为:x2+ +1=2,∵0<x<1,∴认为x2是个较为接近于0的数,令x2≈0,因此省略x2后,得到方程: ,解得,x= ,即
=1+x(0<x<1),可画出如图所示的示意图.由各部分面积之和等于总面积.可列方程为:x2+ +1=2,∵0<x<1,∴认为x2是个较为接近于0的数,令x2≈0,因此省略x2后,得到方程: ,解得,x= ,即![]() =1+x≈ .
=1+x≈ .
(2)请仿照(1)中的方法,若设![]() =1.7+y(0<y<1),求
=1.7+y(0<y<1),求![]() 的近似值(要求画出示意图,标明数据,并将
的近似值(要求画出示意图,标明数据,并将![]() 的近似值精确到千分位)
的近似值精确到千分位)
查看答案和解析>>
科目:初中数学 来源: 题型:
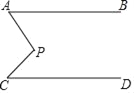
【题目】如图,AB∥CD,∠A=50°,∠C=45°,求∠P的度数.
下面提供三种思路:
(1)过P作FG∥AB
(2)延长AP交直线CD于M;
(3)延长CP交直线AB于N.
请选择两种思路,求出∠P的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上一点,OD平分∠BOC,OE平分∠AOC,则下列说法错误的是( )

A. ∠DOE为直角B. ∠DOC和∠AOE互余
C. ∠AOD和∠DOC互补D. ∠AOE和∠BOC互补
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:抛物线y=- ![]() +bx+c与x轴交于A、B两点,与y轴交于点C,且∠BAC=α,∠ABC=
+bx+c与x轴交于A、B两点,与y轴交于点C,且∠BAC=α,∠ABC= ![]() ,tanα-tanβ=2,∠ACB=90°.
,tanα-tanβ=2,∠ACB=90°.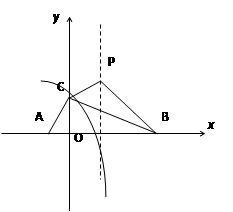
(1)求点C的坐标;
(2)求抛物线的解析式;
(3)若抛物线的顶点为P,求四边形ABPC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com