
【题目】已知AB为⊙O的直径,C为⊙O上一点,AD与过C点的切线垂直,垂足为D,AD交⊙O于点E,∠CAB=30°
(1)如图①,求∠DAC的大小;
(2)如图②,若⊙O的半径为4,求DE的长.
【答案】
(1)解:连接OC,如图①,
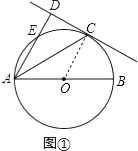
∵DC切⊙O于点C,∴OC⊥DC,又∵AD⊥DC,∴AD∥OC,∴∠DAC=∠ACO,∵OA=OC,∴∠OCA=∠CAB=30°,∴∠DAC=30°;
(2)解:连OE,OC,如图②,

∵∠EOC=2∠DAC=60°,∴△OEC为等边三角形,∴EC=OE=4,∠OCE=60°,∴∠DCE=30°,
∴DE= ![]() CE=2.
CE=2.
【解析】(1):连接OC根据切线的性质定理得出OC⊥DC,又AD⊥DC,根据同一平面内垂直于同一直线的两条直线互相平行得出AD∥OC,根据平行线的性质得出∠DAC=∠ACO,根据等边对等角得出∠OCA=∠CAB=30°,利用等量代换得出结论;
(2)连OE,OC,根据同弧所对的圆心角等于圆周角的2倍得出∠EOC=2∠DAC=60°,根据有一个角为60![]() 的等腰三角形是等边三角形得出△OEC为等边三角形,根据等边三角形三边相等得出EC=OE=4,然后利用含30
的等腰三角形是等边三角形得出△OEC为等边三角形,根据等边三角形三边相等得出EC=OE=4,然后利用含30![]() 角的直角三角形的边角关系得出DE的长。
角的直角三角形的边角关系得出DE的长。
【考点精析】关于本题考查的平行线的判定与性质和含30度角的直角三角形,需要了解由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OE平分∠BOD.
(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.
①用含x的代数式表示∠EOF;
②求∠AOC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点D,OB交半圆于点C,若点C、D、A在量角器上对应读数分别为45°,70°,160°,则∠AOB的度数为;∠A的度数为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列式子:
0×2+1=12……①
1×3+1=22……②
2×4+1=32……③
3×5+1=42……④
……
(1)第⑤个式子 ,第⑩个式子 ;
(2)请用含n(n为正整数)的式子表示上述的规律,并证明:
(3)求值:(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )(1+
)(1+![]() )…(1+
)…(1+![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点P是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C,D.
(1)∠PCD=∠PDC吗?为什么?
(2)OP是CD的垂直平分线吗?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展,小明计划给朋友快递一部分物品,经了解有甲乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)根据题意,填写下表:
重量(千克) | 0.5 | 1 | 3 | 4 | … |
甲公司 | 22 | 67 | … | ||
乙公司 | 11 | 51 | … |
(2)请分别写出甲乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(3)小明应选择哪家快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB,只用圆规找AB的中点P.
作法:
② 以A为圆心,AB长为半径作圆;
②以B为圆心,AB长为半径在圆上连续截取,记截点为B1 , B2 , B3 , B4 , B5;
③ 以B3为圆心,BB3长为半径画弧;以B为圆心,AB长为半径画弧,与前弧交于点C;
④以C为圆心,CB长为半径画弧交线段AB于点P.
结论:点P就是所求作的线段AB的中点.
(1)配合图形,理解作法,根据作图过程给予证明:点P是线段AB的中点.
(2)已知⊙O,请只用圆规把圆周四等分.(保留作图痕迹,不要求写作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的两条对角线相交于点O,过点A作AG⊥BD分别交BD、BC于点G、E. 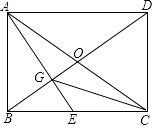
(1)求证:BE2=EGEA;
(2)连接CG,若BE=CE,求证:∠ECG=∠EAC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com