
【题目】某商场在一楼与二楼之间装有一部自动扶梯,以均匀的速度向上行驶,一男孩与一女孩同时从自动扶梯上走到二楼(扶梯本身也在行驶).如果二人都做匀速运动,且男孩每分钟走动的级数是女孩的两倍.又已知男孩走了27级到达顶部,女孩走了18级到达顶部(二人每步都只跨1级).
(1)扶梯在外面的部分有多少级.
(2)如果扶梯附近有一从二楼下到一楼的楼梯,台阶级数与扶梯级数相等,这两人各自到扶梯顶部后按原速度走下楼梯,到一楼后再乘坐扶梯(不考虑扶梯与楼梯间的距离).则男孩第一次追上女孩时,他走了多少台阶?
【答案】(1)楼梯有54级(2) 198级
【解析】【试题分析】
(1)设女孩速度为![]() 级/分,电梯速度为
级/分,电梯速度为![]() 级/分,楼梯(扶梯)为
级/分,楼梯(扶梯)为![]() 级,则男孩速度为
级,则男孩速度为![]() 级/分, 根据时间相等列方程,有:
级/分, 根据时间相等列方程,有:
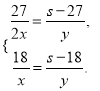 ①两式相除,得
①两式相除,得![]() ,解方程得
,解方程得![]() 即可.
即可.
因此楼梯有54级.
(2)设男孩第一次追上女孩时,走过扶梯![]() 次,走过楼梯
次,走过楼梯![]() 次,则这时女孩走过扶梯
次,则这时女孩走过扶梯![]() 次,走过楼梯
次,走过楼梯![]() 次.
次.
将![]() 代入方程组①,得
代入方程组①,得![]() ,即男孩乘扶梯上楼的速度为
,即男孩乘扶梯上楼的速度为![]() 级/分,女孩乘扶梯上楼的速度为
级/分,女孩乘扶梯上楼的速度为![]() 级/分.于是有
级/分.于是有
![]() 从而
从而![]() ,即
,即![]() .
.
无论男孩第一次追上女孩是在扶梯上还是在下楼时, ![]() 中必有一个为正整数,且
中必有一个为正整数,且![]() ,经试验知只有
,经试验知只有![]() 符合要求.
符合要求.
这时,男孩第一次追上女孩所走过的级数是: ![]() (级).
(级).
【试题解析】
(1)设女孩速度为![]() 级/分,电梯速度为
级/分,电梯速度为![]() 级/分,楼梯(扶梯)为
级/分,楼梯(扶梯)为![]() 级,则男孩速度为
级,则男孩速度为![]() 级/分,依题意有
级/分,依题意有
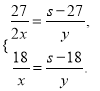 ①
①
把方程组①中的两式相除,得![]() ,解得
,解得![]() .
.
因此楼梯有54级.
(2)设男孩第一次追上女孩时,走过扶梯![]() 次,走过楼梯
次,走过楼梯![]() 次,则这时女孩走过扶梯
次,则这时女孩走过扶梯![]() 次,走过楼梯
次,走过楼梯![]() 次.
次.
将![]() 代入方程组①,得
代入方程组①,得![]() ,即男孩乘扶梯上楼的速度为
,即男孩乘扶梯上楼的速度为![]() 级/分,女孩乘扶梯上楼的速度为
级/分,女孩乘扶梯上楼的速度为![]() 级/分.于是有
级/分.于是有
![]()
从而![]() ,即
,即![]() .
.
无论男孩第一次追上女孩是在扶梯上还是在下楼时, ![]() 中必有一个为正整数,且
中必有一个为正整数,且![]() ,经试验知只有
,经试验知只有![]() 符合要求.
符合要求.
这时,男孩第一次追上女孩所走过的级数是: ![]() (级).
(级).


 小学教材全测系列答案
小学教材全测系列答案科目:初中数学 来源: 题型:
【题目】如图,某学校在“国学经典”中新建了一座吴玉章雕塑,小林站在距离雕塑3米的A处自B点看雕塑头顶D的仰角为45°,看雕塑底部C的仰角为30°,求塑像CD的高度.(最后结果精确到0.1米,参考数据: ![]() ≈1.7)
≈1.7)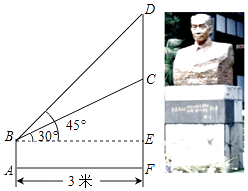
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
解答下列问题:
(1)如果AB=AC,∠BAC=90,当点D在线段BC上时(与点B不重合),如图2,线段CF,BD所在直线位置关系为 ,数量关系为 .
(2)如果AB=AC,∠BAC=90,当点D在线段BC的延长线时,如图3,(1)中的结论是否仍然成立,并说明理由。
(3)如果AB=AC,∠BAC是钝角,点D在线段BC上,当∠ABC满足什么条件时,CF⊥BC(点C、F不重合)画出图形,并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个底面直径为5 cm,高为18 cm的圆柱形瓶内装满水,再将瓶内的水倒入一个底面直径为6cm,高为10cm的圆柱形玻璃中,能否完全装下?若装不下,那么瓶内水面还有多高?若未能装满,求杯内水面离杯口的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元. 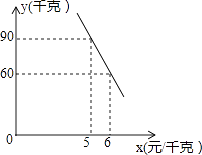
(1)根据题意,填写如表:
(2)经调查,该蔬菜经销商销售该种蔬菜的日销售量y(千克)与零售价x(元/千克)是一次函数关系,其图象如图,求出y与x之间的函数关系式;
(3)若该蔬菜经销商每日销售此种蔬菜不低于75千克,且当日零售价不变,那么零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数学兴趣小组想测量电线杆AB的高度,他们发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4米,BC=10米,CD与地面成30°角,且此时测得1米杆的影长为2米,则电线杆的高度约为米(结果保留根号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料,回答问题:已知(x-2)(6+2x)>0,求x的取值范围.
解:根据题意,得![]() 或
或![]()
分别解这两个不等式组,得x>2或x<-3.
故当x>2或x<-3时,(x-2)(6+2x)>0.
(1)由(x-2)(6+2x)>0,得出不等式组![]() 或
或![]() 体现了____思想.
体现了____思想.
(2)试利用上述方法,求不等式(x-3)(1-x)<0的解集.
附加题(15分,不计入总分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com