
【题目】某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元. 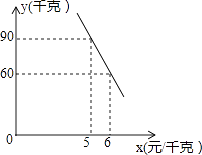
(1)根据题意,填写如表:
(2)经调查,该蔬菜经销商销售该种蔬菜的日销售量y(千克)与零售价x(元/千克)是一次函数关系,其图象如图,求出y与x之间的函数关系式;
(3)若该蔬菜经销商每日销售此种蔬菜不低于75千克,且当日零售价不变,那么零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润为多少元?
【答案】
(1)解:由题意知:当蔬菜批发量为60千克时:60×5=300(元),当蔬菜批发量为90千克时:90×5×0.8=360(元),
填写表格如下:
蔬菜的批发量(千克) | … | 25 | 60 | 75 | 90 | … |
所付的金额(元) | … | 125 | 300 | 300 | 360 | … |
蔬菜的批发量(千克) | … | 25 | 60 | 75 | 90 | … |
所付的金额(元) | … | 125 | 300 | 300 | 360 | … |
(2)解:设该一次函数解析式为y=kx+b(k≠0),
把点(5,90),(6,60)代入,得 ![]() ,
,
解得: ![]() .
.
故该一次函数解析式为:y=﹣30x+240;
(3)解:设当日可获利润w(元),日零售价为x元,由(2)知,
w=(﹣30x+240)(x﹣5×0.8)=﹣30(x﹣6)2+120,
∵﹣30x+240≥75,即x≤5.5,
∴当x=5.5时,当日可获得利润最大,最大利润为112.5元.
【解析】(1)根据这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元,可得60×5=300元;若超过60千克时,批发的这种蔬菜全部打八折,则90×5×0.8=360元;(2)把点(5,90),(6,60)代入函数解析式y=kx+b(k≠0),列出方程组,通过解方程组求得函数关系式;(3)利用最大利润=y(x﹣4),进而利用配方法求出函数最值即可.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,将△AOB绕点B逆时针旋转90°后得到△A′O′B.若反比例函数y= ![]() 的图象恰好经过斜边A′B的中点C,S△ABO=16,tan∠BAO=2,则k的值为( )
的图象恰好经过斜边A′B的中点C,S△ABO=16,tan∠BAO=2,则k的值为( )
A.20
B.22
C.24
D.26
查看答案和解析>>
科目:初中数学 来源: 题型:
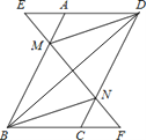
【题目】如图所示,在平行四边形ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点M,N,连接DM,BN.
(1)求证:△AEM≌△CFN;
(2)求证:BD与MN互相平分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场在一楼与二楼之间装有一部自动扶梯,以均匀的速度向上行驶,一男孩与一女孩同时从自动扶梯上走到二楼(扶梯本身也在行驶).如果二人都做匀速运动,且男孩每分钟走动的级数是女孩的两倍.又已知男孩走了27级到达顶部,女孩走了18级到达顶部(二人每步都只跨1级).
(1)扶梯在外面的部分有多少级.
(2)如果扶梯附近有一从二楼下到一楼的楼梯,台阶级数与扶梯级数相等,这两人各自到扶梯顶部后按原速度走下楼梯,到一楼后再乘坐扶梯(不考虑扶梯与楼梯间的距离).则男孩第一次追上女孩时,他走了多少台阶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校合唱团有30名成员,下表是合唱团成员的年龄分布统计表:
年龄(单位:岁) | 13 | 14 | 15 | 16 |
频数(单位:名) | 5 | 15 | x | 10﹣x |
对于不同的x,下列关于年龄的统计量不会发生改变的是( )
A.平均数、中位数
B.平均数、方差
C.众数、中位数
D.众数、方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明、小宇从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小宇骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s(米)与小明出发时间t(分)之间的函数关系如图所示.下列说法:①小宇先到达青少年宫;②小宇的速度是小明速度的3倍;③a=20;④b=600.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘轮船以每小时20千米的速度从甲港驶往160千米远的乙港,2小时后,一艘快艇以每小时40千米的速度也从甲港驶往乙港.分别列出轮船和快艇行驶的路程y(千米)与时间x(小时)的函数关系式,在下图中的直角坐标系中画出函数图象,观察图象回答下列问题:
(1)何时轮船行驶在快艇的前面?
(2)何时快艇行驶在轮船的前面?
(3)哪一艘船先驶过60千米?哪一艘船先驶过100千米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com