练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在Rt△AOB中，两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，将△AOB绕点B逆时针旋转90°后得到△A′O′B．若反比例函数y= 的图象恰好经过斜边A′B的中点C，S△ABO=16，tan∠BAO=2，则k的值为（ ）

    A.20
    B.22
    C.24
    D.26

    【答案】C
    【解析】解：在Rt△AOB中，∵tan∠BAO= =2，
    ∴可以假设OB=2k，OA=k，
    ∴ k2k=16，
    ∴k=4或﹣4（舍弃），
    ∴OA=4，OB=8，
    ∵BC=CA′，
    ∴C（4，6），
    ∵反比例函数y= 的图象经过点C，
    ∴k=24．
    故选C．

    在Rt△AOB中，由tan∠BAO= =2，可以假设OB=2k，OA=k，由题意 k2k=16，推出k=4，可得OA=4，OB=8，C（4，6），由此即可解决问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，△ABC的A、B两个顶点在x轴上，顶点C在y轴的负半轴上．已知|OA|：|OB|=1：5，|OB|=|OC|，△ABC的面积S△ABC=15，抛物线y=ax2+bx+c（a≠0）经过A、B、C三点．

    （1）求此抛物线的函数表达式；
    （2）设E是y轴右侧抛物线上异于点B的一个动点，过点E作x轴的平行线交抛物线于另一点F，过点F作FG垂直于x轴于点G，再过点E作EH垂直于x轴于点H，得到矩形EFGH．则在点E的运动过程中，当矩形EFGH为正方形时，求出该正方形的边长；
    （3）在抛物线上是否存在异于B、C的点M，使△MBC中BC边上的高为 ？若存在，求出点M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

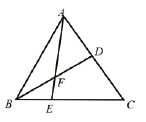
    【题目】如图，在△ABC中E是BC上的一点，EC=2BE，点D是AC的中点，设△ABC，△ADF，△BEF的面积分别为且=24，则=___________

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（10分）在东营市中小学标准化建设工程中，某学校计划购进一批电脑和电子白板，经过市场考察得知，购买1台电脑和2台电子白板需要3．5万元，购买2台电脑和1台电子白板需要2．5万元．

    （1）求每台电脑、每台电子白板各多少万元？

    （2）根据学校实际，需购进电脑和电子白板共30台，总费用不超过30万元，但不低于28万元，请你通过计算求出有几种购买方案，哪种方案费用最低．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在△ABC中，∠ACB为锐角，点D为射线BC上一点，连接AD，以AD为一边且在AD的右侧作正方形ADEF.

    解答下列问题：

    （1）如果AB=AC，∠BAC=90，当点D在线段BC上时(与点B不重合)，如图2，线段CF，BD所在直线位置关系为 ，数量关系为 .

    （2）如果AB=AC，∠BAC=90，当点D在线段BC的延长线时，如图3，（1）中的结论是否仍然成立，并说明理由。

    （3）如果AB=AC,∠BAC是钝角，点D在线段BC上，当∠ABC满足什么条件时,CF⊥BC(点C、F不重合)画出图形,并说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知x=y，则下列各式①x﹣3=y﹣3，②4x=6y，③﹣2x=﹣2y，④，⑤，⑥，其中正确的有（　　）

    A. ①②③ B. ④⑤⑥ C. ①③⑤ D. ②④⑥

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算．

    （1）y=2y﹣1

    （2）5（x﹣5）+2（x﹣12）=0

    （3）y﹣=1﹣

    （4）2（x﹣2）﹣（4x﹣1）=3（1﹣x）

    （5）

    （6）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某蔬菜经销商去蔬菜生产基地批发某种蔬菜，已知这种蔬菜的批发量在20千克～60千克之间（含20千克和60千克）时，每千克批发价是5元；若超过60千克时，批发的这种蔬菜全部打八折，但批发总金额不得少于300元．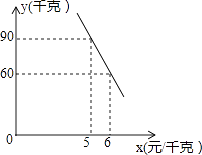
    （1）根据题意，填写如表：
    （2）经调查，该蔬菜经销商销售该种蔬菜的日销售量y（千克）与零售价x（元/千克）是一次函数关系，其图象如图，求出y与x之间的函数关系式；
    （3）若该蔬菜经销商每日销售此种蔬菜不低于75千克，且当日零售价不变，那么零售价定为多少时，该经销商销售此种蔬菜的当日利润最大？最大利润为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，CD⊥AB，EF⊥AB，垂足分别为D、F，∠1=∠2，

    （1）试判断DG与BC的位置关系，并说明理由．

    （2）若∠A=70°，∠BCG=40°，求∠AGD的度数．

    查看答案和解析>>

    同步练习册答案