
【题目】探索发现:如图是一种网红弹弓的实物图,在两头上系上皮筋,拉动皮筋可形成平面示意图如图1图2,弹弓的两边可看成是平行的,即AB∥CD.各活动小组探索∠APC 与∠A,∠C之间的数量关系.已知AB∥CD,点P不在直线AB和直线CD上,在图1中,智慧小组发现:∠APC=∠A+∠C.

智慧小组是这样思考的:过点 P 作 PQ∥AB,……
(1)请你按照智慧小组作的辅助线完成证明过程.
(2)①在图2中,猜测∠APC与∠A,∠C 之间的数量关系,并完成证明.
②如图3,已知AB∥CD,则角α、β、γ之间的数量关系为 .(直接填空)
(3)善思小组提出:如图4,图5.AB∥CD,AF,CF分别平分∠BAP,∠DCP
①在图4中,猜测∠AFC与∠APC之间的数量关系,并证明.
②在图5中,∠AFC与∠APC之间的数量关系为 .(直接填空)

【答案】(1)见解析;(2)①∠APC+∠A+∠C=360°;理由见解析;②α+β-γ=180°;理由见解析;(3)①∠AFC=![]() ∠APC;理由见解析;②∠AFC=180°-
∠APC;理由见解析;②∠AFC=180°-![]() ∠APC;理由见解析;
∠APC;理由见解析;
【解析】
探索发现:由平行线的性质得出∠APQ=∠A,由PQ∥AB,AB∥CD,推出PQ∥CD,得出∠APQ=∠C,推出∠APQ+∠CPQ=∠A+∠C,即可得出结论;
类比思考①过点P作PQ∥AB,延长BA到M,延长DC到N,由平行线的性质得出∠APQ=∠PAM,由PQ∥AB,AB∥CD,推出PQ∥CD,得出∠APQ=∠PCN,则∠APQ+∠CPQ+∠PAB+∠PCD=360°,即可得出结果;
②过点M作MQ∥AB,由平行线的性质得出α+∠QMA=180°,由MQ∥AB,AB∥CD,推出MQ∥CD,得出∠QMD=γ,即可得出结果;
解决问题①过点P作PQ∥AB,过点F作FM∥AB,由平行线的性质得出∠APQ=∠BAP,∠AFM=∠BAF,由角平分线的性质得出∠BAF=∠PAF,即∠AFM=![]() ∠BAP,由PQ∥AB,FM∥AB,AB∥CD,推出PQ∥CD,FM∥CD,得出∠CPQ=∠DCP,∠CFM=∠DCF,由角平分线的性质得出∠DCF=∠PCF,即∠CFM=
∠BAP,由PQ∥AB,FM∥AB,AB∥CD,推出PQ∥CD,FM∥CD,得出∠CPQ=∠DCP,∠CFM=∠DCF,由角平分线的性质得出∠DCF=∠PCF,即∠CFM=![]() ∠DCP,推出∠APC=∠BAP+∠DCP,∠AFC=
∠DCP,推出∠APC=∠BAP+∠DCP,∠AFC=![]() (∠BAP+∠DCP),即可得出结果;
(∠BAP+∠DCP),即可得出结果;
②过点P作PH∥AB,过点F作FQ∥AB,延长BA到M,延长DC到N,由平行线的性质得出∠APH=∠MAP,∠AFQ=∠BAF,由角平分线的性质得出∠BAF=∠PAF,即2∠AFQ=∠BAP,由PH∥AB,FQ∥AB,AB∥CD,推出PH∥CD,FQ∥CD,得出∠CPH=∠NCP,∠CFQ=∠DCF,由角平分线的性质得出∠DCF=∠PCF,即2∠CFQ=∠DCP,由∠BAP+∠MAP=180°,∠DCP+∠NCP=180°,得出2∠AFQ+∠APH=180°,2∠CFQ+∠CPH=180°,即可得出结果.
解:(1)探索发现:∴∠APQ=∠A,
∵PQ∥AB,AB∥CD,
∴PQ∥CD,
∴∠APQ=∠C,
∴∠APQ+∠CPQ=∠A+∠C,
∴∠APC=∠A+∠C;

(2)①∠APC+∠A+∠C=360°;理由如下:
过点P作PQ∥AB,延长BA到M,延长DC到N,如图2所示:
∴∠APQ=∠PAM,
∵PQ∥AB,AB∥CD,
∴PQ∥CD,
∴∠APQ=∠PCN,
∴∠APQ+∠CPQ+∠PAB+∠PCD=180°+180°=360°,
∴∠APC+∠A+∠C=360°,
故答案为:∠APC+∠A+∠C=360°;

②α+β-γ=180°;理由如下:
过点M作MQ∥AB,如图3所示:
∴α+∠QMA=180°,
∵MQ∥AB,AB∥CD,
∴MQ∥CD,
∴∠QMD=γ,
∵∠QMA+∠QMD=β,
∴α+β-γ=180°,
故答案为:α+β-γ=180°;

(3)①∠AFC=![]() ∠APC;理由如下:
∠APC;理由如下:
过点P作PQ∥AB,过点F作FM∥AB,如图4所示:
∴∠APQ=∠BAP,∠AFM=∠BAF,
∵AF平分∠BAP,
∴∠BAF=∠PAF,
∴∠AFM=![]() ∠BAP,
∠BAP,
∵PQ∥AB,FM∥AB,AB∥CD,
∴PQ∥CD,FM∥CD,
∴∠CPQ=∠DCP,∠CFM=∠DCF,
∵CF平分∠DCP,
∴∠DCF=∠PCF,
∴∠CFM=![]() ∠DCP,
∠DCP,
∴∠APC=∠BAP+∠DCP,∠AFC=![]() ∠BAP+
∠BAP+![]() ∠DCP=
∠DCP=![]() (∠BAP+∠DCP),
(∠BAP+∠DCP),
∴∠AFC=![]() ∠APC,
∠APC,
故答案为:∠AFC=![]() ∠APC;
∠APC;

②∠AFC=180°-![]() ∠APC;理由如下:
∠APC;理由如下:
过点P作PH∥AB,过点F作FQ∥AB,延长BA到M,延长DC到N,如图5所示:
∴∠APH=∠MAP,∠AFQ=∠BAF,
∵AF平分∠BAP,
∴∠BAF=∠PAF,
∴2∠AFQ=∠BAP,
∵PH∥AB,FQ∥AB,AB∥CD,
∴PH∥CD,FQ∥CD,
∴∠CPH=∠NCP,∠CFQ=∠DCF,
∵CF平分∠DCP,
∴∠DCF=∠PCF,
∴2∠CFQ=∠DCP,
∵∠BAP+∠MAP=180°,∠DCP+∠NCP=180°,
∴2∠AFQ+∠APH=180°,2∠CFQ+∠CPH=180°,
∴2∠AFQ+∠APH+2∠CFQ+∠CPH=360°,
即2∠AFC+∠APC=360°,
∴∠AFC=180°-![]() ∠APC,
∠APC,
故答案为:∠AFC=180°-![]() ∠APC.
∠APC.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与坐标轴交于A,B两点,则一元二次方程x2+bx+c=0的根的情况是( )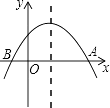
A.没有实数根
B.有两个相等的实数根
C.有两个不相等的实数根
D.可能有实数根,也可能没有实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题1:现有一张△ABC纸片,点D、E分别是△ABC边上两点,若沿直线DE折叠.
(1)探究1:如果折成图①的形状,使A点落在CE上,则∠1与∠A的数量关系是 ;
(2)探究2:如果折成图②的形状,猜想∠1+∠2和∠A的数量关系是 ;
(3)探究3:如果折成图③的形状,猜想∠1、∠2和∠A的数量关系,并说明理由.

(4)问题2:将问题1推广,如图④,将四边形ABCD纸片沿EF折叠,使点A、B落在四边形EFCD的内部时,∠1+∠2与∠A、∠B之间的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 ![]() (
( ![]() 是常数).
是常数).
(1)求证:不论 ![]() 为何值,该函数的图象与x轴没有公共点;
为何值,该函数的图象与x轴没有公共点;
(2)把该函数的图象沿 ![]() 轴向下平移多少个单位长度后,得到的函数的图象与
轴向下平移多少个单位长度后,得到的函数的图象与 ![]() 轴只有一个公共点?
轴只有一个公共点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到![]() ,请解答下列问题:
,请解答下列问题:

(1)图2所表示的数学等式为_____________________;
(2)利用(1)得到的结论,解决问题: 若![]() ,求
,求![]() 的值;
的值;
(3)如图3,将两个边长分别为a和b的正方形拼在一起,![]() 三点在同一直线上,连接
三点在同一直线上,连接![]() ,若两正方形的边长满足
,若两正方形的边长满足![]()
![]() 求阴影部分面积.
求阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD∥AB,点O在AB上,OE平分∠BOD,OF⊥OE,∠D=110°.

(1)求∠DOE的度数;
(2)OF平分∠AOD吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,O是AC、BD的交点,过点O 与AC垂直的直线交边AD于点E,若□ABCD的周长为22cm,则△CDE的周长为( ).

A. 8cm B. 10cm C. 11cm D. 12cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com