
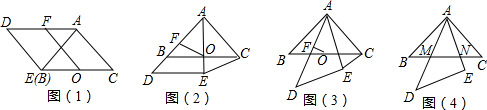
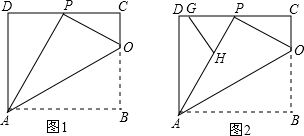
���� ��1����ͼ1������ƽ���ı��ε����ʺ͵���ֱ�������ε�������ü��ɣ���ͼ2�����ݵ���ֱ��������б�����ߵ��������AF=AO������ͨ��֤�á�AFO�ס�AEC���������������ζ�Ӧ�߳ɱ���������ã�
��2����ͼ3��ͨ��֤�á�AFO�ס�AEC���������������ζ�Ӧ�߳ɱ���������ã�
��3����ͼ4�������۵������ʺ�֤�á�AB1N�ա�ACN�ó���AB1N=��C=45�㣬����֤�á�MB1N��ֱ�������Σ�
��� 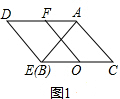 �⣺��1����ͼ1��
�⣺��1����ͼ1��
���ı���ADEC��ƽ���ı��Σ�OΪBC���е㣬FΪAD���е㣬
��OF=AC��
��$\frac{OF}{EC}$=$\frac{AC}{BC}$��
�ߡ�ABCΪ����Rt�����ҡ�BAC=90�㣬
��$\frac{OF}{EC}$=$\frac{AC}{BC}$=$\frac{\sqrt{2}}{2}$��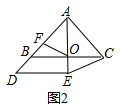
��ͼ2���ڵ���Rt��ADE�У�FΪAD���е㣬
��AF=$\frac{\sqrt{2}}{2}$AE��
�ڵ���Rt��ABC�У�OΪBC���е㣬
��AO=$\frac{\sqrt{2}}{2}$AC����BAO=��CAO=45�㣬
��AE=AC��
��AF=AO��
���AFO�ס�AEC��
��$\frac{OF}{EC}$=$\frac{AO}{AC}$=$\frac{\sqrt{2}}{2}$��
�ʴ�Ϊ$\frac{\sqrt{2}}{2}$��$\frac{\sqrt{2}}{2}$��
��2����ͼ3������AO��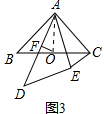
�ڵ���Rt��ADE�У�FΪAD���е㣬
��AF=$\frac{\sqrt{2}}{2}$AE��
�ڵ���Rt��ABC�У�OΪBC���е㣬
��AO=$\frac{\sqrt{2}}{2}$AC����BAO=��CAO=45�㣬
�ߡ�DAE=45�㣬
���DAE=��CAO��
���DAE-��EAO=��CAO-��EAO��
����DAO=��CAE��
��AE=AC��
��AF=AO��
���AFO�ס�AEC��
��$\frac{OF}{EC}$=$\frac{AO}{AC}$=$\frac{\sqrt{2}}{2}$��
��3����ͼ4����������AB=AB1����AB1M=��ABM=45�㣬��BAD=��B1AD��
�ߡ�DAE=45�㣬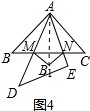
���BAD+��CAE=45�㣬
���B1AD+��CAE=45�㣬
�ߡ�DAE=��B1AM+��B1AN��
���B1AN=��CAN��
��AB=AB1��AB=AC��
��AB1=AC��
�ڡ�AB1N�͡�ACN��
$\left\{\begin{array}{l}{A{B}_{1}=AC}\\{��{B}_{1}AN=��CAN}\\{AN=AN}\end{array}\right.$��
���AB1N�ա�ACN��SAS����
���AB1N=��C=45�㣬
���MB1N=AB1M+AB1N=45��+45��=90�㣬
���MB1N��ֱ�������Σ�
�ʴ�Ϊ��ֱ�������Σ�
���� �����Ǽ��α任�ۺ��⣬������ƽ���ı��ε����ʣ�����ֱ�������ε����ʣ����������Ƶ��ж������ʣ�������ȫ�ȵ��ж������ʣ����������߹��������������ǽ���Ĺؼ���


 ��ѧ�̸̳����¿α�ϵ�д�
��ѧ�̸̳����¿α�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
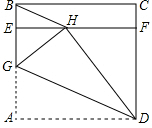 ��ͼ��ABCD��һ�ű߳�Ϊ4cm��������ֽƬ��E��F�ֱ�ΪAB��CD�ϵĵ㣬��BE=CF������EF���ع���D��ֱ�߽���A���ۣ�ʹ�õ�A����EF�ϵĵ�H�����ۺ۽�AE�ڵ�G����BH���ʱ��EG=4-4$\sqrt{2}$cm��
��ͼ��ABCD��һ�ű߳�Ϊ4cm��������ֽƬ��E��F�ֱ�ΪAB��CD�ϵĵ㣬��BE=CF������EF���ع���D��ֱ�߽���A���ۣ�ʹ�õ�A����EF�ϵĵ�H�����ۺ۽�AE�ڵ�G����BH���ʱ��EG=4-4$\sqrt{2}$cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
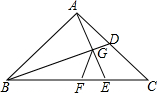 ��ͼ���ڡ�ABC�У�AB=AC����BAC=90�㣬BD�����ߣ�AE��BD����BC�ڵ�E����BD�ڵ�G��BC���е�ΪF������FG
��ͼ���ڡ�ABC�У�AB=AC����BAC=90�㣬BD�����ߣ�AE��BD����BC�ڵ�E����BD�ڵ�G��BC���е�ΪF������FG�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com