
【题目】如图,在平面直角坐标系中,直线![]() 分别交
分别交![]() 轴,
轴,![]() 轴于A,B两点,点C[]为OB的中点,点D在第二象限,且四边形AOCD为矩形.
轴于A,B两点,点C[]为OB的中点,点D在第二象限,且四边形AOCD为矩形.
(1)直接写出点A,B的坐标,并求直线AB与CD交点E的坐标;
(2)动点P从点C出发,沿线段CD以每秒1个单位长度的速度向终点D运动;同时,动点N从点A出发,沿线段AO以每秒1个单位长度的速度向终点O运动,过点P作![]() ,垂足为H,连接NP.设点P的运动时间为
,垂足为H,连接NP.设点P的运动时间为![]() 秒.
秒.
①若△NPH的面积为1,求![]() 的值;
的值;
②点Q是点B关于点A的对称点,问![]() 是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
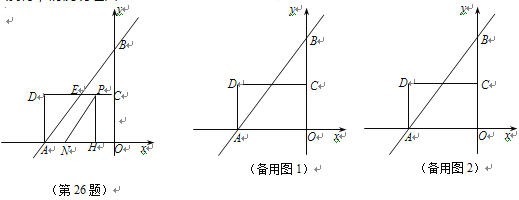
【答案】(1) A(-3,0),B(0,4).![]() (2)①1,2②BP+PH+HQ有最小值,(-2,2)
(2)①1,2②BP+PH+HQ有最小值,(-2,2)
【解析】
试题分析:(1)让y=0求得x的值可得A的坐标,(0,b)为B的坐标,让y=![]() 可得交点的纵坐标,代入直线解析式可得交点的横坐标;
可得交点的纵坐标,代入直线解析式可得交点的横坐标;
(2)由△AMN∽△ABO,得出△MPH的面积,再利用由△HPE∽△HFM,表示出△PEH的面积,即可得出答案.
(3)当点C,H,Q在同一直线上时,CH+HQ的值最小,利用平行四边形的性质得出即可.
试题解析:(1) A(-3,0),B(0,4).
当y=2时,![]()
所以直线AB与CD交点的坐标为![]()
(2)①当0<t<![]() 时,
时,![]()
解得![]()
②当![]() 时,
时,![]()
解得![]()
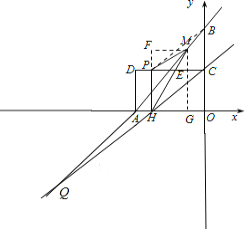
②BP+PH+HQ有最小值.
连接PB,CH,则四边形PHCB是平行四边形.
∴BP=CH.
∴BP+PH+HQ=CH+HQ+2.
当点C,H,Q在同一直线上时,CH+HQ的值最小
∵点C,Q的坐标分别为(0,2),(-6,-4),
∴直线CQ的解析式为y=x+2,
∴点H的坐标为(-2,0).因此点P的坐标为(-2,2)


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 分别交
分别交![]() 轴,
轴,![]() 轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
轴于A,B两点,点C为OB的中点,点D在第二象限,且四边形AOCD为矩形.
(1)直接写出点A,B的坐标,并求直线AB与CD交点E的坐标;
(2)动点P从点C出发,沿线段CD以每秒1个单位长度的速度向终点D运动;同时,动点N从点A出发,沿线段AO以每秒1个单位长度的速度向终点O运动,过点P作![]() ,垂足为H,连接NP.设点P的运动时间为t秒.
,垂足为H,连接NP.设点P的运动时间为t秒.
① 若△NPH的面积为1,求t的值;
② 点Q是点B关于点A的对称点,问![]() 是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
是否有最小值,如果有,求出相应的点P的坐标;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着车辆的增加,交通违规的现象越来越严重,交警对某雷达测速区检测到的一组汽车的时速数据进行整理,得到其频数及频率如表(未完成):
时速数据段 | 频数 | 频率 |
30﹣40 | 10 | 0.05 |
40﹣50 | 36 | ___ |
50﹣60 | ___ | 0.39 |
60﹣70 | ___ | ___ |
70﹣80 | 20 | 0.10 |
总计 | 200 | 1 |
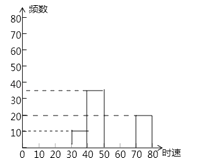
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果汽车时速超过60千米即为违章,则这次检测到的违章车辆共有 辆.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点P在△ABC的边AC上,下列条件中,不能判断△ABP∽△ACB的是( )

A.∠ABP=∠C B.∠APB=∠ABC C.AB2=APAC D.![]() =
=![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com