
【题目】如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了5.2米到达点C,然后沿斜坡CD前进,到达坡顶D点处,DC=BC.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角∠AEF为27°(点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)i=1:2.4,求建筑物AB的高度.(参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)

科目:初中数学 来源: 题型:
【题目】如图,专业救助船“沪救1”轮、“沪救2”轮分别位于A、B两处,同时测得事发地点C在A的南偏东60°且C在B的南偏东30°上.已知B在A的正东方向,且相距100里,请分别求出两艘船到达事发地点C的距离.(注:里是海程单位,相当于一海里.结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面内容:我们已经学习了《二次根式》和《乘法公式》,聪明的你可以发现:当![]() ,
,![]() 时,∵
时,∵![]() ,∴
,∴![]() ,当且仅当
,当且仅当![]() 时取等号.请利用上述结论解决以下问题:
时取等号.请利用上述结论解决以下问题:
(1)当![]() 时,
时,![]() 的最小值为_______;当
的最小值为_______;当![]() 时,
时,![]() 的最大值为__________.
的最大值为__________.
(2)当![]() 时,求
时,求![]() 的最小值.
的最小值.
(3)如图,四边形ABCD的对角线AC ,BD相交于点O,△AOB、△COD的面积分别为4和9,求四边形ABCD面积的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
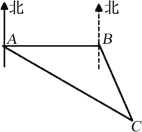
【题目】将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.
(1)求证:AF+EF=DE;
(2)若将图①中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其它条件不变,请在图②中画出变换后的图形,并直接写出你在(1)中猜想的结论是否仍然成立;
(3)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其它条件不变,如图③.你认为(1)中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
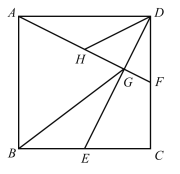
【题目】如图,在边长为4的正方形![]() 中,点
中,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,![]() 、
、![]() 交于点
交于点![]() ,
,![]() 的中点为
的中点为![]() ,连接
,连接![]() 、
、![]() .给出下列结论:①
.给出下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论有________.(请填上所有正确结论的序号)
.其中正确的结论有________.(请填上所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】河南省开封市铁塔始建于公元1049年(北宋皇祐元年),是国家重点保护文物之一,在900多年中,历经了数次地震、大风、水患而巍然屹立,素有“天下第一塔”之称.如图,小明在铁塔一侧的水平面上一个台阶的底部A处测得塔顶P的仰角为45°,走到台阶顶部B处,又测得塔顶P的仰角为38.7°,已知台阶的总高度BC为3米,总长度AC为10米,试求铁塔的高度.(结果精确到1米,参考数据:sin38.7°≈0.63,cos38.7°≈0.78,tan38.7°≈0.80)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 在平面直角坐标系中, ![]() 的顶点
的顶点![]() 与原点重合,点
与原点重合,点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() 按以下步骤作图:①以点
按以下步骤作图:①以点![]() 为圆心,适当长度为半径作
为圆心,适当长度为半径作![]() 弧,分别交边
弧,分别交边![]() ,
,![]() 于点
于点![]() ,
,![]() ;②分别以点
;②分别以点![]() ,
,![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧, 两弧在
的长为半径作弧, 两弧在![]() 内交于点
内交于点![]() ;③作射线
;③作射线![]() ,交边
,交边![]() 于点
于点![]() .若
.若![]() ,
,![]() ,则点
,则点![]() 的坐标为( )
的坐标为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校“校园主持人大赛”结束后,将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图.部分信息如下:
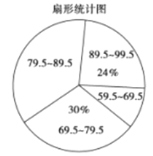
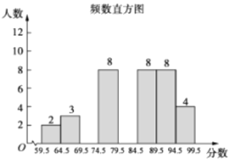
(1)本次比赛参赛选手共有________人,扇形统计图中“79.5~89.5”这一范围的人数占总参赛人数的百分比为________;
(2)补全图2频数直方图;
(3)赛前规定,成绩由高到低前40%的参赛选手获奖.某参赛选手的比赛成绩为88分,试判断他能否获奖,并说明理由;
(4)成绩前四名是2名男生和2名女生,若他们中任选2人作为该校文艺晚会的主持人,试求恰好选中1男1女为主持人的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com